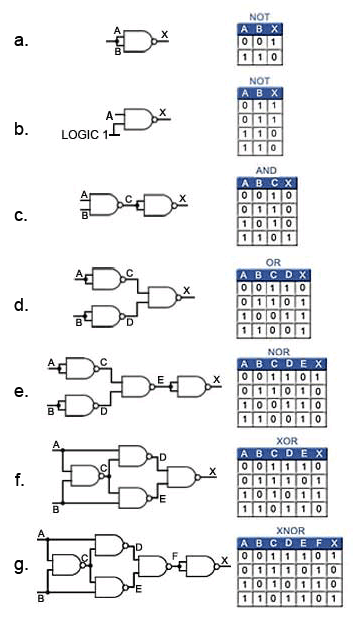
|  |
For 2 logical inputs, there are 16 possible logic gates. Table 1 defines the 16 logic gates, shows logical symbol, behavior in symbolic logic, provides name, notes.
People are most familiar with the ones that are named: NAND, NOR, AND, OR, XOR. Table 1 includes these, as well as AND and OR gates with either input negated, logic 0 and logic 1(which aren't really logic gates), and some gates that aren't really binary.
| Output when AB is | ||||||||
| Gate # | 00 | 01 | 10 | 11 | Symbolic Logical Description | Symbol | Name/Description | Note |
| 0 | 0 | 0 | 0 | 0 | 0 |  |
Always zero | Not really a gate |
| 1 | 0 | 0 | 0 | 1 | A & B |  |
AND | |
| 2 | 0 | 0 | 1 | 0 | A & ~B |  |
A and Not B | Universal |
| 3 | 0 | 0 | 1 | 1 | A | 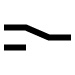 |
A | Not BInary |
| 4 | 0 | 1 | 0 | 0 | ~A & B | 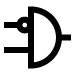 |
B and Not A | Universal |
| 5 | 0 | 1 | 0 | 1 | B |  |
B | Not Binary |
| 6 | 0 | 1 | 1 | 0 | (A & ~B) | (~A & B) |  |
XOR | Also Not Equals Function |
| 7 | 0 | 1 | 1 | 1 | A | B | 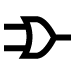 |
OR | |
| 8 | 1 | 0 | 0 | 0 | ~(A | B) |  |
NOR | Universal |
| 9 | 1 | 0 | 0 | 1 | (A & B) | (~A & ~B) |  |
XNOR | Also Equals Function |
| 10 | 1 | 0 | 1 | 0 | ~B |  |
Not B | Not Binary |
| 11 | 1 | 0 | 1 | 1 | A | ~B |  |
A or Not B | Universal |
| 12 | 1 | 1 | 0 | 0 | ~A | 
|
Not A | Not Binary |
| 13 | 1 | 1 | 0 | 1 | ~A | B |  |
B or Not A | Unversal |
| 14 | 1 | 1 | 1 | 0 | ~(A & B) |  |
NAND | Universal |
| 15 | 1 | 1 | 1 | 1 | 1 |  |
Always 1 | Not really a gate |
Examples (a)-(g) below demonstrate how one can use a universal gate (here, the NAND gate) to construct several other gates: