• About
• Statistics
• Number Theory
• Java
• Data Structures
• Cornerstones
• Calculus

Searching and Sorting Arrays

Searching Arrays

One of the most common tasks associated with arrays is searching through them to find some desired element.

Linear Searches

Suppose we wish to write a method that takes in a one-dimensional array and some value x, and returns either the position (i.e., "index") of x in the array, or -1 if x does not appear in the array.

One option would be to use a linear search. In a linear search, we compare x (which we call the "key") with each element in the array list, starting at one end and progressing to the other. Graphically, we can imagine the following comparisons being made:

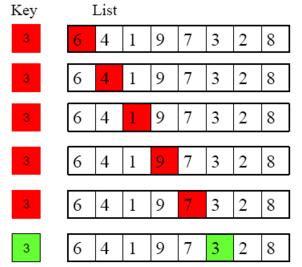
Supposing that our array is an array of integers, we might use the following method to accomplish this linear search:

public static int linearSearch(int[] list, int key) {
   for (int i = 0; i < list.length; i++)
       if (key == list[i])
           return i;  //found it! so we immediately exit the method
   return -1;     //didn't find it, but we have to return something
}

Below, we call the above method on an example array, using a few different key values.

int[] list = {1, 4, 4, 2, 5, -3, 6, 2};
int pos1 = linearSearch(list, 4);    //pos1 now equals 1
int pos2 = linearSearch(list, -4);   //pos2 now equals -1
int pos3 = linearSearch(list, -3);   //pos3 now equals 5

Binary Searches

Linear Searches work well, but when used on arrays with a large number of elements, they potentially have to check every element to find a match. This can take a while, especially if we are doing multiple such searches.

There is a way to speed things up substantially, however -- provided that the elements in the array are ordered. (Let us assume for the sake of the discussion below that they are in ascending order).

A binary search works on an ordered list, and first compares the key with the element in the middle of the array. (In the case of an even number of elements in our list, we will use the element that ends the first half of the list as our "middle element").

• If the key is less than the middle element, we only need to search the first half of the array, so we continue searching on this smaller list.
• If the key is greater than the middle element, we only need to search the second half of the array, so we continue searching on this smaller list.
• If the key equals the middle element, we have a match -- end the search

The diagram below illustrates how a key value of 8 is found in an ordered list in just 3 steps:

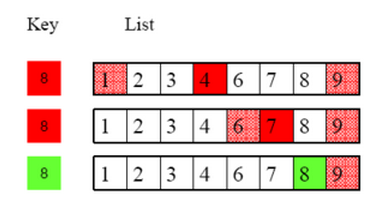
Note how we keep track of the sublist we are actually searching by keeping track of its left-most and right-most elements.

1. Initially, we are searching the entire list, so the left-most element is 1, while the right-most element is 9. There is an even number of elements in our list, so as mentioned above, we use the element that ends the first half of the list as our "middle element" (i.e., the "4").
2. Since 4 is less than the key value 8, we only need to search the second half of the list from 1 to 9. As such, we update the left-most element of the list searched to be the "6", while we leave the right-most element of the list searched unchanged (it's still the 9). The "middle element" of this sublist, which again has an even number of elements, is again taken as the element that ends the first half of this sublist from 6 to 9, which is 7.
3. Since 7 is still less than the key value 8, we again only need to search the second half of the sublist from 6 to 9. As such, we update the left-most element of the sublist searched to be the 8, while we leave the right-most element of the sublist searched unchanged (it's still the 9). The "middle element" of this sublist, which again has an even number of elements, is again taken to be the element that ends the first half of this sublist from 8 to 9, which is 8. (Note, as the sublist only has two elements, following the aforementioned rule for finding "middles", gives us a middle for this sublist identical to the "left-most" element of this sublist.)
4. Since 8 equals the key value, we stop the search, we have found what we were looking for!

Of course, we need to be keeping track of the indices of each of the elements, so we know what position to return, when we are all done.

Here's an example of a binary search for 11 in the given list, that keeps track of index of the left-most element (i.e., the "lowest index" to consider), the index of the right-most element (i.e., the "highest index" to consider), and the index of the element in the "middle" of these two positions:

The search method in the above example should then return a value of 4, the index of the found key value.

Here's another example, where we are searching for a key value of 54:

Notice when we check if list[7] equals the key in the last step, and discover that 54 < 59, we must conclude that the key value -- if present -- would be left of list[7], in an area of the main list that was already eliminated. This, of course can't be -- so we know that key is not present in the list.

However, the position we found is still useful. We made an assumption with the binary search method that our list was in ascending order. For this to be true, one of two things must have happened -- either we sorted the list (which can be computationally expensive), or we never let our list get out of order in the first place. That is to say, every time we added a value to the list, we made sure we inserted it in just the right spot to preserve the order. Note, "just left" of list[7] is right where we would want to insert the key value of 54, Thus, we might have our search method not just return a negative value (like -1), to indicate the absence of the key value in the list, but also build into that negative value some useful information, like the index where the key value should be inserted.

Here's how this algorithm might look as code:

public static int binarySearch(int[] list, int key) {
   int low = 0;
   int high = list.length - 1;

   while (high >= low) {           //the loop only stops when
                                   //high gets updated to something
                                   //it shouldn't       
  
      int mid = (low + high) / 2;  //note what this does
                                   //if (low + high) is odd
   
      if (key < list[mid])         //update index of the 
         high = mid - 1;           //right-most element considered 
                                
      else if (key > list[mid])    //update index of
         low = mid + 1;            //left-most element considered
                                
      else
         return mid;               //found it! now return the 
                                   //index and exit the method

   }

   return -1 - low;  //key was not found, so
                     //return negative value
                     //that doubles as an insertion
                     //point when turned back
                     //to a positive value
}

Below are some examples of its use.

public static void main(String[] args) {
  int[] list1 = {3, 4, 7, 10, 11, 45, 50, 59, 60, 66, 70};
  System.out.println("Index is " + binarySearch(list1,11));
  //prints "Index is 4"

  int[] list2 = {3, 4, 7, 10, 45, 50, 59, 60, 66, 70};
  System.out.println("Index is " + binarySearch(list2,11));
  //prints "Index is -5"
  
  int[] list3 = {3, 4, 7, 10, 45, 50, 59, 60, 66, 70};
  System.out.println("Index is " + binarySearch(list3,2));
  //prints "Index is -1"
}

Note that when the key is not found, we can recover the insertion index by adding 1 to the returned value and removing the negative sign. So in the second call to binarySearch above, when we get a -5 back, we know that 11 was not in the list (as the return value was negative) and if we wanted to add it, it should be put at and index of -(-5+1) (i.e., 4) in our list.

The reason for the offset of 1 (observe the line return -1 - low; in the code above) becomes clear when looking at the last call to binarySearch above -- without it, the method would return a zero, leading one to believe that 2 was actually in the list!

There is a limitation to the method that we wrote above to implement a binary search -- it only works on lists whose elements are of type int. Fortunately, a more expansive binarySearch method that works on arrays of a variety of types is available to us: java.util.Arrays.binarySearch()

Consider the following example of its use:

char[] chars = {'a', 'c', 'g', 'x', 'y', 'z'};
System.out.println("Index is " + 
   java.util.Arrays.binarySearch(chars, 't'));

//Prints "Index is -4", which tells us 't' 
//is not in the list, but could be inserted 
//at index 3

Note: for the java.util.Arrays.binarySearch() method to work properly, the array passed to it must be pre-sorted in ascending order.

Sorting Arrays

The binary search method, in both of the implementations discussed above required the array be pre-sorted. What if that's not the case? How can we take an unsorted array and sort it?

Turns out, there are a number of ways we could do this...

The Selection Sort

One algorithm for sorting an array, called the selection sort, focuses on finding minimum (or alternatively, maximum) values and moving them to one end of the list.

Here's the basic idea:

1. We search through the entire list to find the smallest element, and then swap that element with the first element of the list.
2. Now we know the first element is in the correct position (as far as sorting goes), so we focus our attention on the rest of the list (i.e., everything but the first element). We search through just this shorter list to find the smallest element it contains, and then swap this element with the second element of our main list.
3. Now we know the first two elements are in the correct position (as far as sorting goes), so we focus our attention on the rest of the list (i.e., everything but the first two elements). We search through this yet shorter list to find the smallest element it contains, and then swap this element with the third element of our main list.
4. We continue in this way until all but the last element of the list have been correctly placed... Of course, once everything else is in the correct spot, the remaining last element must be in the right spot too. The list is now sorted.

Let's see what an array might look like at various stages of this process:

Below is one possible way to code this sorting method:

import java.util.Arrays;

public class SortingFun {
	
  public static void exch(int[] a, int i, int j) {
    int temp = a[i];
    a[i] = a[j];
    a[j] = temp;
  }

  public static void selectionSort(int[] a) {
    int n = a.length;
    for (int i = 0; i < n; i++) {
      int minPos = i;
      for (int j = i+1; j < n; j++) {
        if (a[j] < a[minPos]) {
           minPos = j;
        }
      }
      exch(a,i,minPos);
      System.out.println(Arrays.toString(a));
    }
  }

  public static void main(String[] args) {
    int[] a = {4, 9, 1, 2, 3, 7, 5, 8, 6};
    selectionSort(a);
    System.out.println(Arrays.toString(a));
  }
}

The Insertion Sort

Another algorithm for sorting an array is known as the insertion sort. Here, one sorts a list of values by repeatedly inserting an unsorted element into a sorted sublist until the whole list is sorted.

Again, perhaps it is best to explain by an example:

Below is one way to implement an insertion sort for an array of elements of type int.

import java.util.Arrays;

public class SortingFun {
	
  public static void exch(int[] a, int i, int j) {
    int temp = a[i];
    a[i] = a[j];
    a[j] = temp;
  }

  public static void insertionSort(int[] a) {
    int n = a.length;
    for (int i = 0; i < n; i++) {
      for (int j = i; j > 0; j--) {
        if (a[j] < a[j-1]) 
          exch(a, j, j-1);
        else 
          break;
      }
      System.out.println(Arrays.toString(a));
    }
  }

  public static void main(String[] args) {
    int[] a = {4, 9, 1, 2, 3, 7, 5, 8, 6};
    insertionSort(a);
    System.out.println(Arrays.toString(a));
  }
}