Operations on Binary Search Trees Involving Key Order

Imagine you are writing a program to store and review security camera footage for some business. The camera in question only records video when it detects movement in its field of vision. To be able to quickly pull the video for any requested time, you decide to store the recorded clips in a binary search tree, using the time-stamps on the videos as the keys.

However, you realize that if you ever had to work with the police to review the video footage, they may not know the exact times of the videos they want to see. Instead, they may ask questions like:

How far back do your recordings go?
What's the last thing you recorded?
What's the last video you have at or before 10:30pm last night?
What's the next thing you recorded after this video?

Note how all of these questions involve finding keys relative to other keys. In the first two questions, we seek the minimum and maximum key (e.g., first and last times). In the third question, we want to find the largest key possible (e.g., the latest time) that is less than or equal to a given key (e.g., at or before 10:30 PM). In the last, we must find the next larger key (e.g., the key for the very next video).

Questions like these, involving finding keys in some relative order to other keys, are common in a variety of applications. Fortunately, finding their answers when the keys are stored in a binary search tree tree can be accomplished using some very efficient operations, as we will see below...

Finding the minimum and maximum keys

Consider where the minimum and maximum keys in a binary search tree are located. It shouldn't take long to realize that they correspond to the left-most and right-most nodes, respectively, as suggested by the below image.

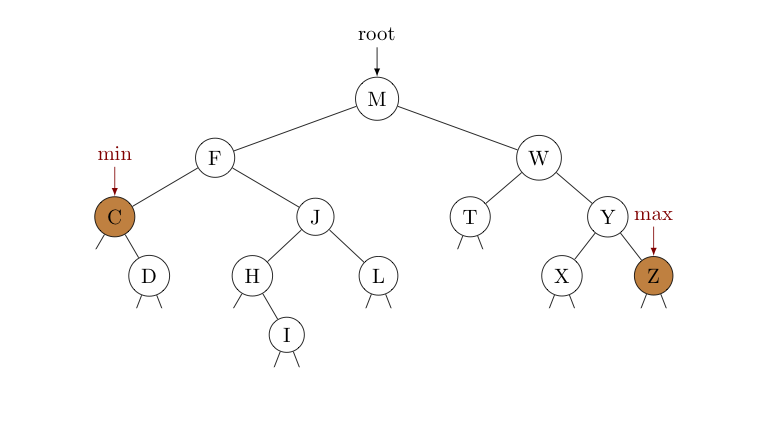
Finding these keys is simple. To locate the minimum, start with a reference equal to the root and just keep updating it to be its own left child until that left child is null. To find the maximum we do the same thing, but with the right child. An iterative solution for finding the minimum is shown below -- similar code can be used to find the maximum.

public Key minKey() {
    Node n = root;

    if (n == null) return null;  // if empty tree, min does not exist!

    while (n.left != null)       // while you can go left,
        n = n.left;              // go left

    return n.key;
}

Of course, we can attack the problem recursively as well, using our standard two-method approach to keep from exposing the Node class to the client.

public Key minKey() {             // public-facing method where Node class 
   return minKey(root).key;       // is not exposed
} 

private Node minKey(Node n) {     // private method to handle recursion via subtrees..

   if (n == null) return null;    // if empty tree, min does not exist!

   if (n.left == null) return n;  // nothing is left of n, so nothing smaller (base case)

   return minKey(n.left);         // there are keys less than n's key to the left, 
                                  // so recurse on left subtree 
}

Finding the Floor of a Key

The largest key less than or equal to some key $k$ is called the "floor" of $k$. The image below shows floor values for various keys.

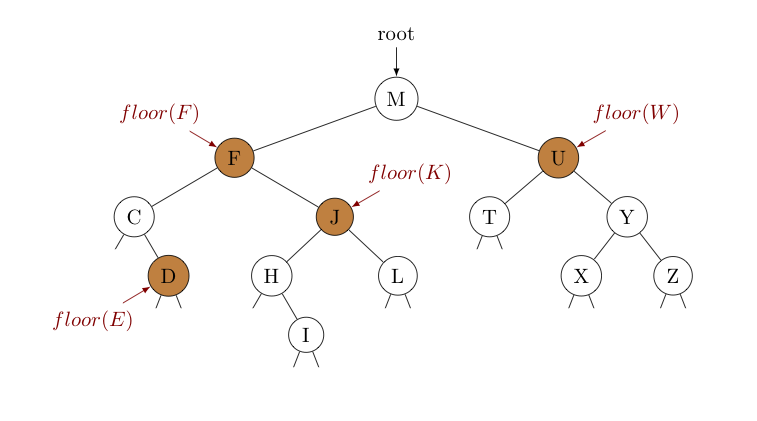
Let's consider each of these examples in turn, to discover the common questions we'll need to ask to navigate from the root to the floor for a given key in a recursive way:

$floor(F)$
We consider the root first, noting $F \lt M$. This tells us it must be in the left subtree. Noting this subtree is rooted at $F$, we have found the floor of $F$.
$floor(E)$
Starting again with the root, we see $E \lt M$. So again it must be in the left subtree (rooted at $F$). Since $E \lt F$, it must likewise be in the subtree rooted at $C$. Seeing $C \lt E$ however, we aren't immediately sure. The floor of $E$ could be $C$ itself, but if we can find any (larger) key in the right subtree that is still $\le E$, it will be in this right subtree (rooted at $J$) instead. Seeing the lone key $D \le E$ in this right subtree, this must be the floor of $E$.
$floor(K)$
Starting at the root, we have $K \lt M$, so it must be in the left subtree (rooted at $F$). As $F \lt K$, it could be that $F$ is the floor of $K$, or if there is any (larger) key in the right subtree still $\le K$, the floor will be in this right subtree (rooted at $J$ instead. Of course, $J \le K$, so the floor of $K$ is not $F$. It could be that it is $J$, but only if we can't find a (larger) key still $\le K$ in the right subtree of $J$. There is only $L \gt K$ in this right subtree, so the floor of $K$ must indeed be $J$.
$floor(W)$
Observing $M \lt W$ at the root, it could be that $M$ is the floor of $W$, but only if we can't find a (larger) key still $\le W$ in the right subtree rooted at $U$. As $U \le W$, the floor must not be $M$. It could be this $U$, but only if we can't find a (larger) key still $\le W$ in the right subtree rooted at $Y$. As it happens, we can't find key $\le W$ in this last subtree, so the floor of $W$ must actually be $U$.

As the above examples demonstrate, computing the floor of a given key $k$ requires a comparison with the key from each node examined, taking one of the following actions, as appropriate:

If $k$ agrees with the node key, the floor of $k$ is simply $k$.
If $k$ is smaller than the node key, then the floor of $k$ must be in the left subtree. Recurse on this subtree.
If $k$ is greater than the node key, then the node's key is the floor of $k$ only if we can't find a (larger) key still $\le k$ in the right subtree.

These 3 rules form the basis of the recursive implementation of floor(Key key) given below:

public Key floor(Key key) {
  Node n = floor(root, key);
  if (n == null) return null;
  return n.key;
}

private Node floor(Node n, Key key) {
  if (n == null) return null;                              //empty trees don't have floors!

  int cmp = key.compareTo(n.key);

  if (cmp == 0) return n;                                        // we found the floor! 

  if (cmp < 0) return floor(n.left, key);                        // key < node key, so it's
                                                                 // in the left subtree 

  Node floorInRightSubTree = floor(n.right, key);                // maybe this node key is 
  if (floorInRightSubTree != null) return floorInRightSubTree;   // the floor, or maybe it's 
  else return n;                                                 // in the right subtree --
                                                                 // need to check!
}

Just as the floor of a key is the largest key less than or equal to it, the ceiling of a key is the smallest key greater than or equal to it. The technique for finding a ceiling mirrors that used to find a floor.

As one might guess, given that we are again simply navigating downwards through the tree one level at a time, finding both the floor and ceiling of a given key is $O(\ln n)$.