|  |
A graph is an interesting and useful mathematical structure that can describe a network of connections between pairs of nodes. They provide an extremely useful abstraction for representing data in a variety of contexts and practical applications.
In a graph, we refer to the nodes as vertices, and the connections between pairs of vertices we call edges.
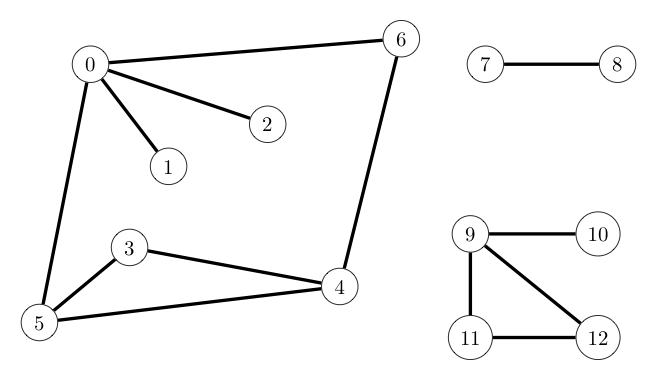
We can gain some intuition about the structure of a graph by drawing it as a collection of labeled dots (vertices) and connecting lines (edges). However, one should be aware that any given graph can be drawn in many different ways, as the graphic below demonstrates. The specific positions of the nodes is generally not relevant. We instead focus solely on the connections between the nodes present. As can be seen below, these are preserved despite the nodes being drawn in different places.
 |
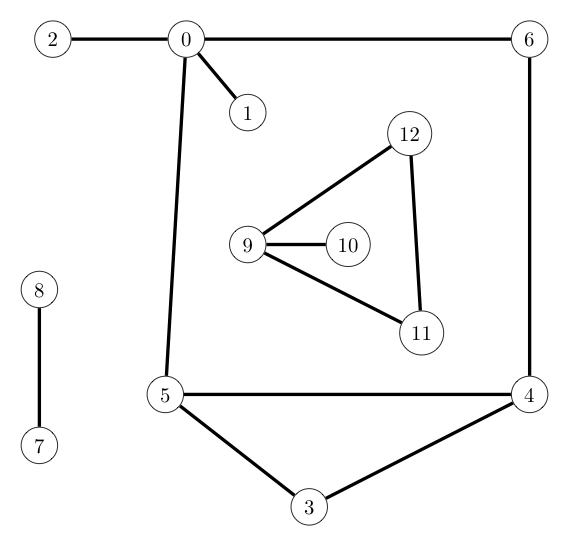 |
Two drawings of the same graph
The following notes some specific contexts in which the use of graphs can be helpful, noting specifically what plays the role of a vertex and what plays the role of an edge in each:
| Context | Vertex | Edge |
|---|---|---|
| communication | telephone, computer | fiber optic cable |
| electric circuits | gate, register, processor | wire |
| transportation | intersection | road |
| board game | game piece position | legal move |
| social network | person | friendship |
| neural network | neuron | synapse |
| map | state, country | shared border |
| molecule | atom | bond |
| protein network | protein | protein-protein interaction |
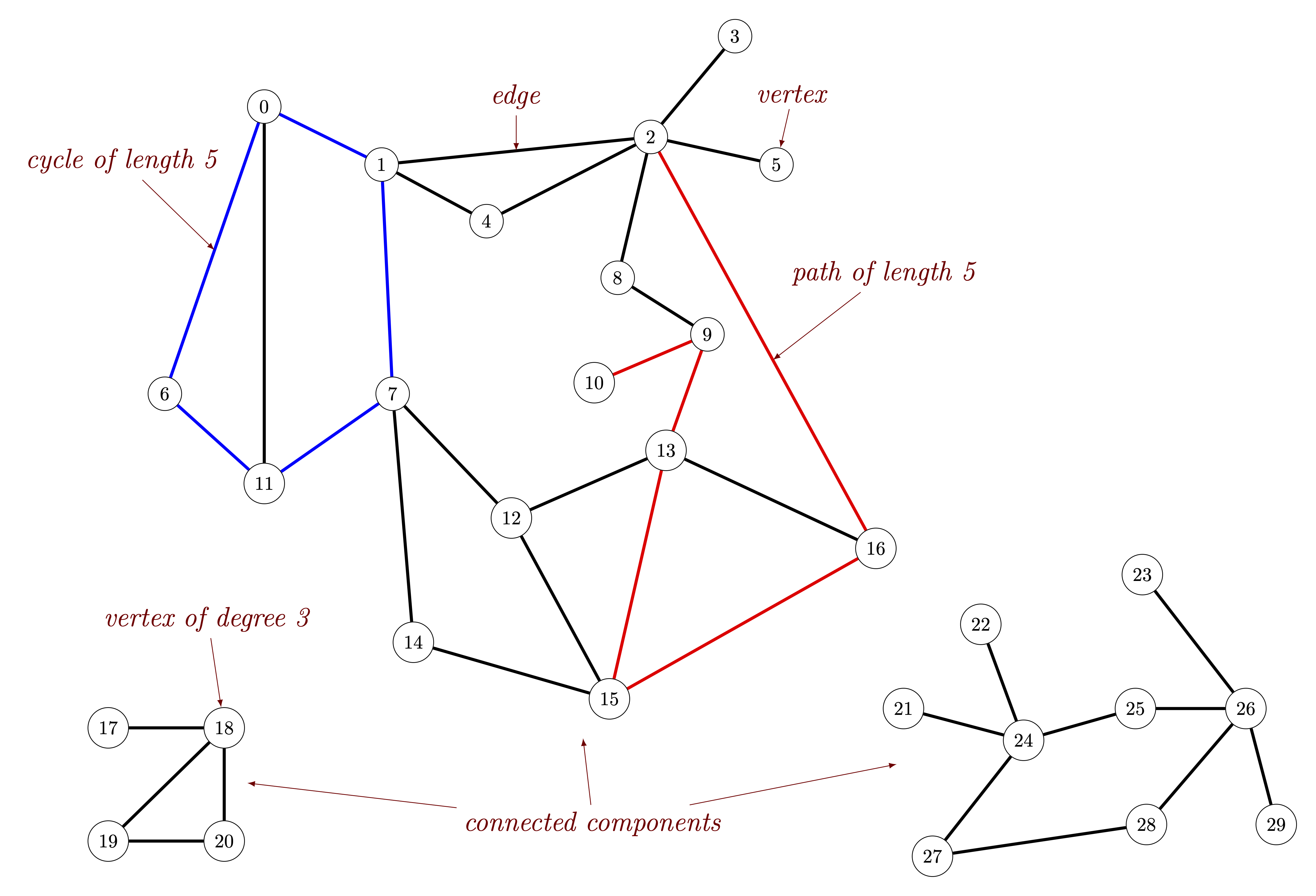
In a graph, when there is an edge connecting two vertices, the vertices are said to be adjacent to one another and the edge is incident to both vertices. Similarly, adjacent edges are edges that share a common vertex. As some examples seen in the graph below, vertices $3$ and $4$ are adjacent, while $1$ and $6$ are not. Further, edge d is incident to vertices $0$ and $6$, but is not incident to any other vertices, although it is adjacent to edges $a$, $e$, $f$, and $c$.

Two edges that connect the same pair of vertices are called parallel, while an edge that connects a vertex to itself is called a loop. The degree of a vertex is the number of edges incident to that vertex, with loops counted twice. So, the degree of vertex $0$ in the graph below is $5$, while the degree of vertex $1$ in the same graph is $3$.
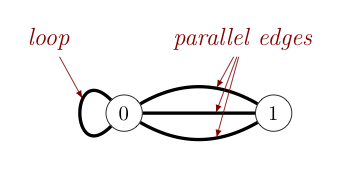
A subgraph is a subset of a graph's edges (and associated vertices) that constitutes a graph.
A path in a graph is a sequence of vertices connected by edges. A simple path is one with no repeated vertices. When the first and last vertices of a path (of at least one edge) are the same, we call the path a cycle. A simple cycle is a cycle with no repeated vertices or edges (except the first and last vertices). An graph is said to be acyclic if it contains no cycles. The length of a path or cycle is its number of edges.
One vertex is said to be connected to another if there exists a path that contains them both. More generally, we say a graph is connected if there is a path from every vertex in the graph to every other vertex in the graph. Note, that a graph that is not connected necessarily consists of a set of connected components. As an example, note how the graph on $29$ vertices below is a set of three connected components (of $4$, $16$, and $9$ vertices).