

 |  |
We've seen how to insert a key-value pair into a binary search tree. How do we remove such a pair? In other words, how do we delete a node from a binary search tree?

In order to accomplish the swap, we'll not only need a reference to this successor, but we'll also need to delete it from the aforementioned right subtree. We can use the min(Node n) method from the previously discussed recursive implementation of min() to get the reference to the successor. As for deleting it from the right subtree, let's create a separate method deleteMin(Node n) that will delete the node with minimum key in the subtree whose top-most node is n and return a reference to the deleted node.
Creating this deleteMin() is easy to do recursively, as shown below. Note that as a node is removed, the counts of nodes in the affected subtrees must be updated.
Take a moment and convince yourself this code does what it says.
private Node deleteMin(Node n) {
if (n.left == null) // current node is the min
return n.right;
n.left = deleteMin(n.left); // there are nodes smaller than
// the current node (and they are
// to the left)
n.count= 1 + size(n.left)+ size(n.right); // update count of nodes at or
// below this one
return n;
}
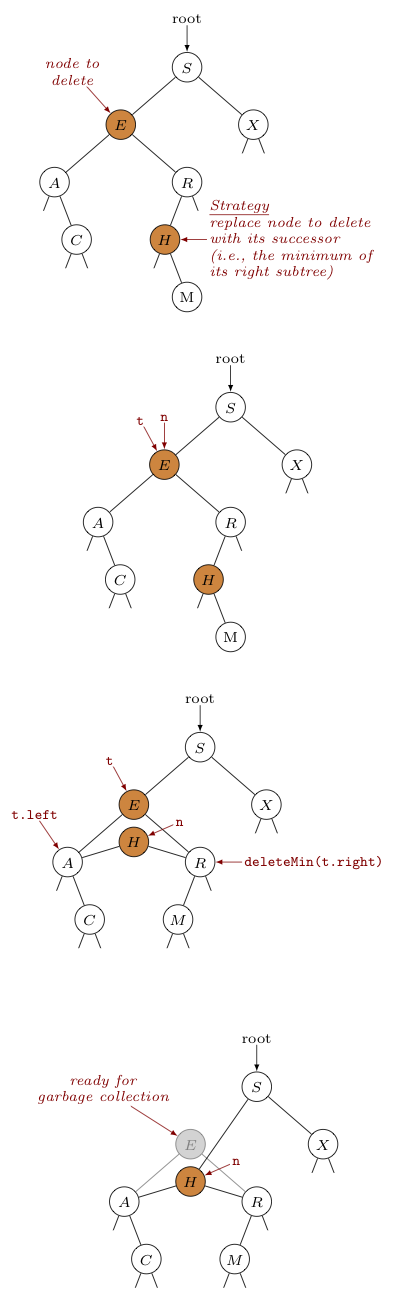
With the above method in hand, consider the code below for deleting a node by swapping it with its successor, along with a specific example of its application shown on the right -- where we remove node $E$ from the tree shown.
public void delete(Key key) {
root = delete(root, key);
}
private Node delete(Node n, Key key) {
if (n == null) // there is nothing
return null; // to delete
int cmp = key.compareTo(n.key);
if (cmp < 0) // key < n.key,
n.left = delete(n.left, key); // so search left
else if (cmp > 0) // key > n.key,
n.right = delete(n.right, key); // so search right
else { // key == n.key
// found it! node to
// delete is n
if (n.right == null) // n has no right child,
return n.left; // so return left child
// note, if n has no
// left child either
// this returns null
Node t = n; // protect n from garbage
// collection. we'll need
// it later...
n = min(t.right); // let n get the key and
// value of the minimum
// node in the right
// subtree -- this will
// be the successor of
// the previous n. we'll
// update the left and
// right links next...
n.right = deleteMin(t.right); // removes the
// aforementioned
// successor from the
// right subtree of the
// old n (stored in t)
// then this tree is put
// to the right of the
// new n.
n.left = t.left; // make the new n's
// left link the same
// as the original n's
// left link
}
n.count = size(n.left) + // update the count
size(n.right) + 1; // for this new n
// Note: deleteMin()
// updated other
// counts affected
return n;
}
|
 |