

 |  |
In the realm of coding theory one defines a code as a means for replacing certain symbols, or sequences of symbols (called words), in a message with other symbols, or sequences of symbols. Contrary to popular usage of the term, these "codes" are rarely intended to keep their encoded messages secret. While they have a variety of other applications, one frequently finds them used in techniques related to data compression.
Consider the following "gen-z" tweet, which suggests a useful analogy:
Spps y wrt n ntrstng stry. Spps t ws th bst stry y hd vr wrttn. Nw tk tht splndd stry nd rs ll th vwls.
For those that don't partake in twitter or IM, reading the above might take a moment -- but it should ultimately be readable. To generate the message above, we have -- in the interest of shortening how much one has to type -- replaced the words we intended to write with "code words" constructed by removing any and all vowels encountered in our intended words. By doing this, we shorten the message from its original length of 147 characters (shown below) down to 106 characters.
Suppose you wrote an interesting story. Suppose it was the best story you had ever written.
Now take that splendid story and erase all the vowels.
Huffman coding provides a similar means to reduce the space required to store information -- counted not in characters, but in bits. In the example to come, we will take the following message, which in ASCII requires 368 bits to encode (remember each character requires 8 bits, and there are 46 characters in this message), and store it with Huffman encoding in only 115 bits -- quite the improvement!
"A DEAD DAD CEDED A BAD BABE A BEADED ABACA BED"In case you are wondering about the strange and slightly morbid nature of the message, know that it was chosen so that the number of symbols used (six, counting the space) would be small, which will make our example easier to follow.
The basic strategy used to accomplish this reduction is to replace characters that frequently occur with bitstrings that are shorter than those used to replace characters that occur less frequently.
However, in a bitstring everything is a 1 or a 0. Without a fixed number of bits per character, it may be difficult to determine where one bitstring stops and another begins. The use of delimeters (like spaces or commas) can help, but they add to the length of the message -- which is at cross purposes with what we hoped to do. A Huffman code solves this problem in a different way. It is known as a prefix-free code where the bitstring representing some particular symbol is never a prefix of a bitstring representing any other symbol.
The technique works by creating a binary tree of nodes, similar to a max-heap. Initially, all nodes are leaf nodes which each contain a symbol and a weight equal to the frequency with which that symbol appears. The process then takes the two nodes with the smallest weight (notably, an operation for which a min-heap-based priority queue might be useful) and creates a new node which contains the symbols found in these two nodes and has these two nodes as children. The weight of the new node is set to the sum of the weights of its children. We then apply the process again on the new node and the remaining nodes (i.e., we exclude the two leaf nodes). We repeat this process until only one node remains, which is the root of the Huffman tree. Steps #2 through #6 below show how this plays out on the aforementioned string (i.e., the one about a "beaded abaca bed"), seen again in step #1.
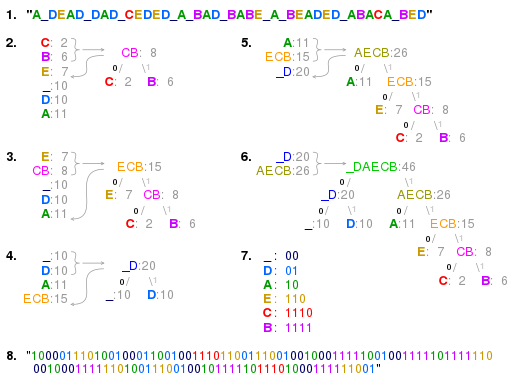
Once the tree is constructed, we can navigate from the root to any given symbol by going left or right at each level depending on which child includes the symbol in question. We write a $0$ every time we go left and a $1$ every time we go right, until we terminate at the leaf containing the symbol. The resulting bitstring is the code for that symbol, which can then be cached for speed in later use.
Note that step #7 above shows the codes constructed from the Huffman tree for the characters found in the "abaca bed" message, while step #8 shows the bitstring that results from replacing each letter of the original message with its corresponding code.
Decoding once the tree is constructed is simple as well. Reading some long bitstring of ones and zeros from left to right, one simply starts at the root of the tree and navigates left or right down the tree depending on whether a zero or one was read, respectively. Upon reaching a leaf of the tree, one decodes the ones and zeros read so far as the symbol stored in that leaf -- and then repeat the process, starting over again at the root, with the rest of the ones and zeros in the bitstring.