

 |  |
Consider the following two trees:

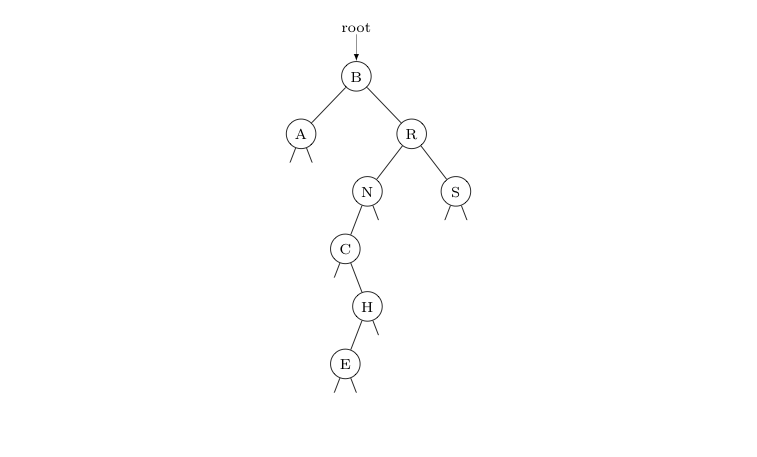
Starting with an empty binary search tree, nodes with keys B, R, A, N, C, H, E, and S are are inserted into the tree in that order. Draw the final state of the tree produced.
How many binary tree shapes of $n$ nodes are there with height $n-1$?
$2^{n-1}$ as one can go left or right towards each of the remaining $n-1$ nodes from the root node.
Given a BST in pre-order as $\{13, 5, 3, 2, 11, 7, 19, 23\}$, draw this BST and determine if this BST is the same as one described in post-order as $\{2, 3, 5, 7, 11, 23, 19, 13\}$.
Remembering a BST must be in symmetric order, the BST initially described is given by
|
+---------13--+
| |
+--5-----+ 19--+
| | |
+--3 +--11 23
| |
2 7
In post-order, this tree would be described by $\{2,3,7,11,5,23,19,13\}$. So this is a different BST then the one described in post-order in the question.
Part of a binary search tree class (BST) is given below. Complete the lines marked A-E below so that put(Key key,Value val) inserts the key/value pair into the BST if it is not already present, and updates the value otherwise. In doing so, do not create or reference any methods or instance variables beyond the ones provided below.
public class BST, Value> { private class Node { private Key key; private Value val; private Node left; private Node right; public Node(Key key, Value val) { this.key = key; this.val = val; } } private Node root; public void put(Key key, Value val) { __________________________ /* Line A */ private Node put(Node n, Key key, Value val) { if (n == null) { return new Node(key, val); } int cmp = key.compareTo(n.key); if (cmp < 0) _________________________ /* Line B */ else if (cmp > 0) _________________________ /* Line C */ else _________________________ /* Line D */ _________________________ /* Line E */ } . . . }
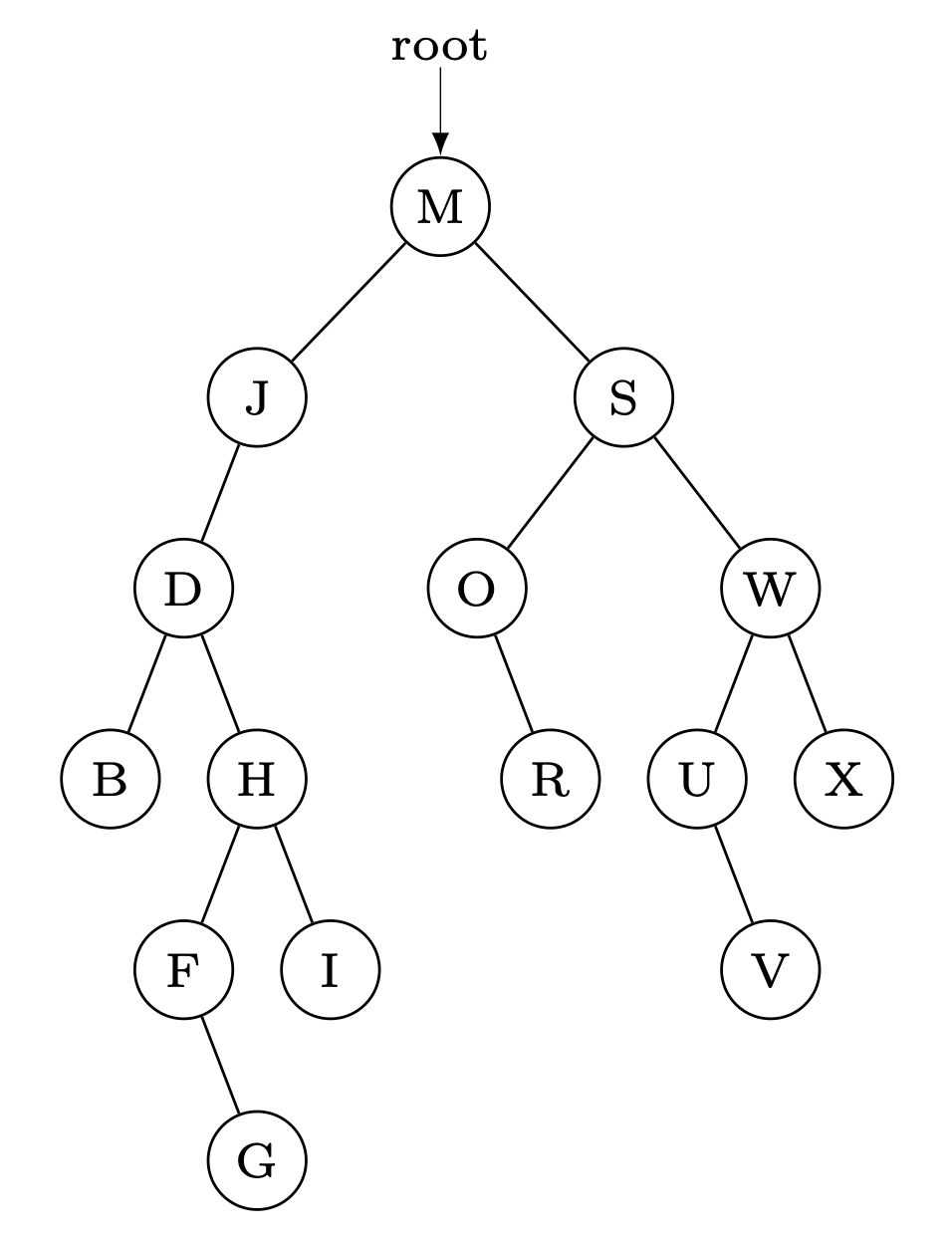
root = put(root, key, val)n.left = put(n.left, key, val);n.right = put(n.right, key, val);n.val = val;return n;For the binary search tree below, show the three states of the tree after the Hibbard deletion (using successors) of nodes corresponding to keys I, E, and S, in that order, respectively.
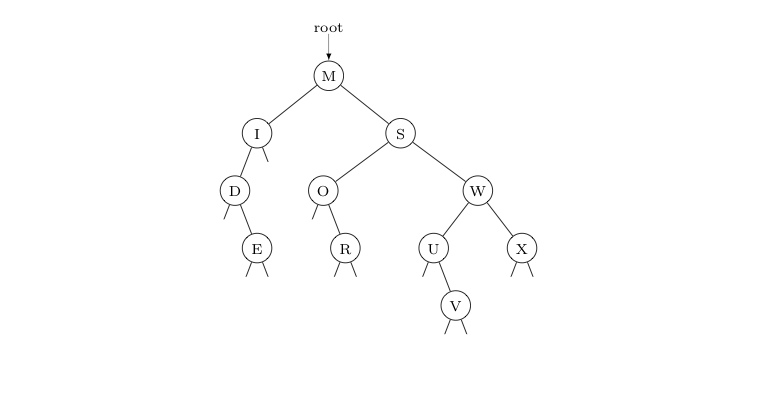
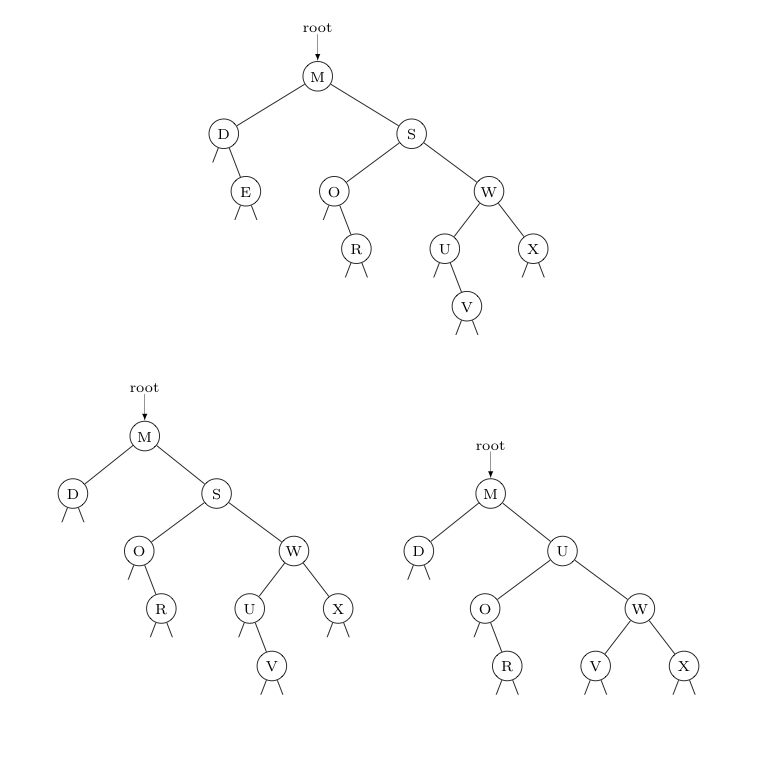
In the binary search tree given below, show the three states of the tree after the Hibbard deletion (using successors) of nodes corresponding to keys X, O, and D, in that order, respectively.
deleting X:
|
+--M--------+
| |
+--------------J- +-----S--------+
| | |
+--D--------+ -O--+ +-----W-
| | | |
-B- +-----H--+ -R- -U--+
| | |
-F--+ -I- -V-
|
-G-
deleting O:
|
+--M-----+
| |
+--------------J- +--S--------+
| | |
+--D--------+ -R- +-----W-
| | |
-B- +-----H--+ -U--+
| | |
-F--+ -I- -V-
|
-G-
deleting D:
|
+--M-----+
| |
+-----------J- +--S--------+
| | |
+--F-----+ -R- +-----W-
| | |
-B- +--H--+ -U--+
| | |
-G- -I- -V-
Complete the class BstChecker so that the isBst(Node root) method returns true if and only if the tree rooted at root is a binary search tree (i.e., a binary tree in symmetric order). You may assume all values in the nodes of the tree are unique positive integers.
public class BstChecker {
// INSERT VARIABLE DECLARATIONS HERE, AS DESIRED...
private static class Node {
int value;
Node left;
Node right;
Node(int value) {
this.value = value;
left = null;
right = null;
}
}
public boolean isBst(Node root) {
// INSERT CODE HERE...
}
// INSERT ADDITIONAL METHODS HERE, AS DESIRED...
public static void main(String[] args) {
Node r1 = new Node(13);
r1.left = new Node(5);
r1.right = new Node(19);
r1.left.left = new Node(3);
r1.left.left.left = new Node(2);
r1.left.right = new Node(11);
r1.left.right.left = new Node(7);
r1.right.right = new Node(23);
// Note, as defined above, r1 is a BST
Node r2 = new Node(13);
r2.left = new Node(5);
r2.right = new Node(12);
r2.left.left = new Node(6);
r2.left.left.left = new Node(2);
r2.left.right = new Node(11);
r2.left.right.left = new Node(7);
r2.right.right = new Node(23);
// Note, as defined above, r2 is not a BST
BstChecker bstChecker = new BstChecker();
System.out.println(bstChecker.isBst(r1) ? "Is a BST" : "Not a BST");
System.out.println(bstChecker.isBst(r2) ? "Is a BST" : "Not a BST");
}
}
Complete the class BinaryTreeInOrderIterable so that it fully supports the Iterable interface with iteration producing the keys in order (i.e., from least to greatest, as dictated by their implementation of the Comparable interface).
In doing so, you may add instance variables, as needed, to the anonymous class implementing the Iterator interface -- but do not add any additional methods to this anonymous inner class. Also refrain from adding any instance variables or methods to the outer class. As one final, but important limitation - accomplish this task without the use of recursion.
To traverse a binary tree in level order means to start at the root, and then visit all nodes one node away from the root (starting with the left node, if not null); and then visit all nodes two nodes away from the root (again, left-most to right-most), as they exist; and then visit all nodes 3 nodes away from the root and so on...
The following is a modified version of the binary search tree class developed elsewhere in these notes : BST.java. This new version includes an additional method named keysLevelOrder(), intended to return a queue of the keys of the binary search tree in level order.
Complete this class by adding an appropriate body to this method. Do not add any instance variables or other methods to the class besides this one.
You will need to include in your project the QueueArray class and the Queue interface it implements. These are, of course, necessary for the rest of the BST class to function, but you may find them very useful in implementing this new method as well.
You can use the LevelOrderTest class to test your code. A sample run is shown below:
$ java LevelOrderTest↵ Enter a sequence of letters (all uppercase) to be inserted into a binary search tree: FGCEHBDA↵ Level Order = FCGBEHAD