| | |
Rational values (i.e., "fractions") are quotients of integers. When one finds the decimal form of a rational value via the process of long division, sometimes there are no decimal places needed to be written in the result (i.e., the denominator evenly divided the numerator); sometimes there are only a finite number of (non-zero) decimal places in the result, and sometimes there are an infinite number of (non-zero) decimal places. However, one can prove that when a rational value has an infinite number of (non-zero) decimal places, some subsequence of the digits that result must ultimately start repeating (and never stop).
As you should be aware -- most programming languages' primitive types for floating-point values can only store a close approximation to most of the values they could be assigned. For example, if one executes the statement System.out.println(1691.0/330.0); in a Java program, you will see the approximation 5.12424242424242424 (in which the sequence of digits "24" repeats only 8 times) instead of the exact value, where the sequence of digits "$24$" is repeated an infinite number of times.
In mathematics, to indicate that a digit sequence repeats an infinite number of times, we typically write a bar over those digits. Armed with this notation, we can write the exact value for the previously mentioned fraction of $1691⁄330$ as $5.1\overline{24}$
With these thoughts in mind and your knowledge of how to conduct long division by hand, complete the class Division by adding code to the body to its fractionAsDecimal() method, allowing it to perform the appropriate long divison so that it can output the string that gives the decimal form associated with its input exactly -- using the "over-bar" notation just described, as needed.
You may assume the user only enters fractions of positive integers, with each separated by a single space. You may also assume the user never enters a denominator equal to zero.
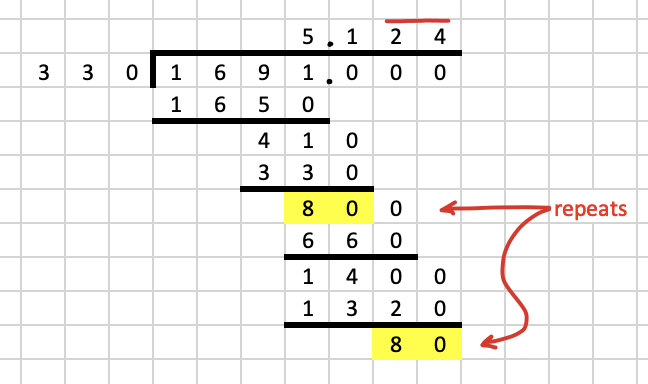
Importantly, in the process of long division, one should recall that the instant one sees the same amount left after two subtractions in that algorithm, one knows that the digit sequence of the quotient will start repeating from that point forwards.
As an example, note how in the following long division we see the difference of $1400-1320 = 80$ repeat the previous difference of $410-330=80$. Then take note of the values subtracted below, starting at the first $80$ (turned into $800$ by bringing one of the zeros "down"). The first was $660$, which is $2$ times the divisor (i.e., $330$ here). The second is $1320$, which is $4$ times the divisor. As such, the digits of $2$ and $4$ seen at top will necessarily repeat ad infinitum from this point forward. We can easily see this if we continue with the long division algorithm any further. We add an over-bar to these digits to indicate this repetition (drawn in red, below), which completes the process.
As it relates to printing your output in the terminal with an "over-bar" drawn over some digits, you may also find it helpful to know that this can be accomplished by appending the unicode character U+0305 to the relevant character (or characters) in a string.
As an example, to print $5.1\overline{24}$, use the following string -- which will draw two small bars (which connect) over the 2 and the 4:
"5.12" + "\u0305" + "4" + "\u0305"
Below is a sample run of the Division class. Note: to see the output displayed correctly in both your browser and your IDE or console, you need to be using a font that supports Unicode standards. The default fonts on a Mac do this automatically. On a Windows machine, you may need to temporarily adjust the font to "Lucida Sans Unicode", before it looks correct. (Just don't leave your browser or IDE using this font as a permanent replacement for a fixed-width font, as it is not one.)
$ java Division↵ Enter some number of fractions of positive integers (separated by spaces). Long division will then be used to find their (exact) decimal forms. 8/2 3/2 1/8 1/7 101/3 1/6 1/12 970/23 1691/330 3179893/9906↵ 8/2 = 4 3/2 = 1.5 1/8 = 0.125 1/7 = 0.1̅4̅2̅8̅5̅7̅ 101/3 = 33.6̅ 1/6 = 0.16̅ 1/12 = 0.083̅ 970/23 = 42.1̅7̅3̅9̅1̅3̅0̅4̅3̅4̅7̅8̅2̅6̅0̅8̅6̅9̅5̅6̅5̅2̅ 1691/330 = 5.12̅4̅ 3179893/9906 = 321.00̅6̅7̅6̅3̅5̅7̅7̅6̅2̅9̅7̅1̅9̅3̅6̅2̅0̅0̅2̅8̅2̅6̅5̅6̅9̅7̅5̅5̅7̅0̅3̅6̅1̅3̅9̅7̅1̅3̅3̅0̅5̅
The tower of Hanoi was a popular puzzle of the late nineteenth century. The puzzle includes three pegs and some number of rings of different sizes placed in order of size, with the largest on the bottom, on one of the pegs. The goal of the puzzle is to move all the rings, one at a time without ever placing a larger ring on top of a smaller ring, from the first peg to the second, using the third peg as an auxiliary peg.
Complete the Java class TowersOfHanoi so that one can play this game in the terminal by simply typing two digits at a time (each chosen from either 0, 1, or 2), indicating from which pile to remove a disk and to which pile it should be added, respectively.
Illegal moves should be called out by displaying "ILLEGAL MOVE" upon their attempt, and upon winning (by getting all the disks in pile 0 moved to pile 2, the text "YOU DID IT!" should be printed.
You may find it helpful to know that the disks first drawn (top-down) consist of 1, 3, 5, 7, ... unicode block characters (specifically, "\u2587") concatenated together, respectively. As such, the entire state of the game at any point could be described by a 2d-array with one dimension indicating the tower (i.e., 0, 1, or 2) to which a given disk belongs and the other representing the (vertical) level on which that disk can be found (with 0 being the bottom, 1 being the next level up, 2 being the next), with the entries in that array indicating the number of block characters for the disk in question.
Below is a sample run, played by a user that can't follow directions very well (to help ensure your program can identify illegal moves).
$ java TowersOfHanoi↵ How many disks do you want to use? 3↵ Goal: Move all the disks from pile 0 to pile 2 Restrictions: You can only move a top-most disk from one pile onto another pile that is either empty or whose top-most disk is larger than the one moved To move a disk from pile X to pile Y: Type 'XY' and then hit 'enter' ▇ ▇▇▇ ▇▇▇▇▇ ===================== 0 1 2 02↵ ▇▇▇ ▇▇▇▇▇ ▇ ===================== 0 1 2 02↵ ILLEGAL MOVE 01↵ ▇▇▇▇▇ ▇▇▇ ▇ ===================== 0 1 2 21↵ ▇ ▇▇▇▇▇ ▇▇▇ ===================== 0 1 2 20↵ ILLEGAL MOVE 01↵ ILLEGAL MOVE 02↵ ▇ ▇▇▇ ▇▇▇▇▇ ===================== 0 1 2 13↵ ILLEGAL MOVE 10↵ ▇ ▇▇▇ ▇▇▇▇▇ ===================== 0 1 2 12↵ ▇▇▇ ▇ ▇▇▇▇▇ ===================== 0 1 2 02↵ ▇ ▇▇▇ ▇▇▇▇▇ ===================== 0 1 2 YOU DID IT!
Recalling that a recursive method is one that invokes itself in its own definition/body, one should know that every recursive method can be re-written to use an iterative approach instead (i.e., accomplishing the same task without recursion, typically by using loops). The same works in reverse. Every method using an iterative approach can be be re-written to use a recursive one instead. This is perhaps a surprising duality, and upon learning about stacks and another special data structure known as a graph, we will be able to investigate further how exactly a programmer can always construct one from the other.
At this moment however, we consider a special case of recursive methods -- methods using tail recursion -- and how these can be easily translated into efficient iterative methods.
"Tail recursion" describes the implementation of a recursive algorithm when the recursive call is the last operation in the method before returning. Nicely, tail-recursive methods don't require a stack or graph to implement iteratively. They can get by with a simple "accumulator" instead. For those unfamiliar with the term, an accumulator is simply a register, or a memory location (think "variable") used to store intermediate results of arithmetic or logical operations. This can greatly reduce the memory required by the calculation from what might be required by a stack, and as such increase the efficiency and performance of the method. Indeed, many compilers upon seeing a tail-recursive method will optimize the code by effectively swapping it out with an equivalent iterative method towards the same end. In this problem, we explore a task structurally similar to that faced by the aforementioned compilers.
Consider the code given in the interface ProblemSpecAndTools, along with class TailRecursionToIteration. Put both in a package named twoways and then add code that involves no recursion to the body of the method findIteratively() in the TailRecursionToIteration class, to make this method always agree in output with the findRecursively() method of that same class. Make sure to test your work before proceeding!
After finding success with the above, use the given inner static class FactorialPSAT of the TailRecursionToIteration as a template and complete the other two inner classes appearing (i.e., StringReverserPSAT and GcdPSAT) so that they can be used in conjunction with the TailRecursionToIteration to reverse a given string of text and to calculate the gcd (i.e., greatest common divisor) of two numbers, respectively.
You can use the class TailRecursionToIterationTest class to test your results (as long as you put it in the same package). A sample run of this testing class is shown below. Again, when your findIteratively() method is correct, its output -- regardless of whether you are finding factorial, reversing a string, or calculating a gcd -- should always match that of the findRecursively() method for the same task.
$ java TailRecursionToIterationTest↵ Enter a positive integer n to see the value of n! 10↵ 3628800 3628800 Enter a string of text to see it reversed the quick brown fox jumped over the lazy dog↵ god yzal eht revo depmuj xof nworb kciuq eht god yzal eht revo depmuj xof nworb kciuq eht Enter two positive integers to find their greatest common divisor (gcd) 54321↵ 9876↵ 3 3
Let $f(x)$ be defined for a given integer $x$ as the number resulting from removing any right-most even digits $x$ might have until either an odd digit is encountered or only a single digit remains. For a given sequence of integers $\{ x_0, x_1, x_2, \ldots, x_n \}$, we wish to find the sum $$\sum_{i=0}^n f(x_{n-i})$$ Towards this end, write a class StrangeSum that when run, prompts the user to enter some sequence of integers separated by spaces, and then prints the summation sought, first as an expanded sum of the corresponding $f$ values, and then as the simplified total. These two expressions should be separated by an equals sign, as shown in the sample run below.
Importantly, note that the subscript of $(n-i)$ in the summation above means that the order in which the $f$ values should be shown in the first expression should agree with applying $f$ to the numbers entered in reverse order.
Here's a sample run:
$ java StrangeSum↵ Enter two or more integers to add, separated by spaces 2 3 40 52 682 794 900↵ 9+79+6+5+4+3+2=108
Strikingly, when one starts with $41$ at the center, an unbroken string of $40$ primes fall on the main diagonal (from the position of $1523$, through that of $41$, and extending to the position of $1601$). This is the longest known unbroken string of primes on a diagonal of such a spiral.
Create a tool to investigate what Ulam discovered. Write a class PrimeSpiral that when run, prompts the user to enter a positive integer $n$ and an odd number $m$. Then, the class should print an $m \times m$ grid of tab-delimited values from $n$ to $m^2+n-1$ that follow a rectangular spiral starting with $n$ in the center-most position of the grid, with $(n+1)$ is to the immediate right of this value, and with subsequent consecutive values spiraling counterclockwise, as suggested by the sample run below.
For easy identification, print an asterisk immediately following every prime number in the grid. For those that might have forgotten, the value $1$ is not prime.
Here's a sample run that allows us to see a portion of the primes on Ulam's spiral (starting at $41$):
$ java PrimeSpiral↵ Enter a positive starting number and an odd number of rows/columns, separated by a space: 41 11↵ 141 140 139* 138 137* 136 135 134 133 132 131* 142 105 104 103* 102 101* 100 99 98 97* 130 143 106 77 76 75 74 73* 72 71* 96 129 144 107* 78 57 56 55 54 53* 70 95 128 145 108 79* 58 45 44 43* 52 69 94 127* 146 109* 80 59* 46 41* 42 51 68 93 126 147 110 81 60 47* 48 49 50 67* 92 125 148 111 82 61* 62 63 64 65 66 91 124 149* 112 83* 84 85 86 87 88 89* 90 123 150 113* 114 115 116 117 118 119 120 121 122 151* 152 153 154 155 156 157* 158 159 160 161
You must include (and use) two methods in the PrimeSpiral class:
isPrime(int num) which returns true when num is prime, and false when it is not.numAt(int row, int col, int n, int m) which returns the number that should be displayed in the specified row and column for a spiral that starts at $n$ and consists of $m^2$ values arranged as indicated earlier.Traditionally, we write integer values using the decimal system, where each digit stands for a multiple of a power of $10$, which is the number of different digit symbols available to us (i.e., $0$ through $9$). We generally call this number of digits available to us the "base", or sometimes the "radix" (the Latin word for "root", and thus a synonym in this sense). As the power of the base $10$ associated with a given digit depends upon the position of the digit in the number in question, we say the decimal system a positional numeral system.
The choice of $10$ as our base and number of digits clearly stems from our having ten fingers and ten toes ("finger or toe" translates to the Latin digitus, after all). Had spiders developed mathematics instead of humans and given the number of legs they have, they might have adopted a "base $8$" system instead (using only digits $0$ to $7$, and powers of $8$) -- and everything would have still worked out just fine. In fact, the base can be chosen to be any integer from $2$ to infinity -- each will lead to an effective way to denote integers. In computer science, base $2$ (binary) and base $16$ (hexadecimal) are particularly important. Indeed, one might find it valuable to know that Java has built-in support for converting from one base to another. The interested reader can consult the Java API regarding the methods parseInt(String s, int radix) and toString(int i, int radix) in the Integer class to learn more.
There are other less familiar systems for denoting integers, however -- many of which are not supported in any standard Java libraries. One of these is called factoradic notation. The name here merges the words "factorial" and "radix", given that it is a positional numeral system where we add multiplies of factorials (instead of powers), with the coefficients on these factorials written in base/radix $10$.
More specifically, a number written in factoradic form typically appears as a sequence of base $10$ values separated by colons, such as $$3\!:\!4\!:\!1\!:\!0\!:\!1\!:\!0$$ To find the integer value associated with the factoradic form, we multiply each value between colons from left to right by decreasing factorials, down to $0!$ (much like in base $10$ we multiply the digits left to right by decreasing powers of $10$, down to $10^0$) and then sum the resulting products together, as the example below demonstrates: $$\begin{array}{rcl} 3\!:\!4\!:\!1\!:\!0\!:\!1\!:\!0 &=& 3 \cdot 5! + 4 \cdot 4! + 1 \cdot 3! + 0 \cdot 2! + 1 \cdot 1! + 0 \cdot 0!\\ &=& ((((3 \cdot 5 + 4)\cdot 4 + 1)\cdot 3 + 0)\cdot 2 + 1)\cdot 1 + 0\\ &=& 463 \end{array}$$ (Note, the calculation of the equivalent expression seen in the second line above avoids redundant multiplications present in the first, and is thus much more efficient. Make sure to take advantage of this observation in the class you are about to be asked to write.)
Converting from base $10$ back to factoradic form is essentially a reversal of the calculations found in the second line above, as we can see below: $$\begin{array}{rcl} 463 \div 1 &=& 463 \textrm{, remainder } 0\\ 463 \div 2 &=& 231 \textrm{, remainder } 1\\ 231 \div 3 &=& 77 \textrm{, remainder } 0\\ 77 \div 4 &=& 19 \textrm{, remainder } 1\\ 19 \div 5 &=& 3 \textrm{, remainder } 4\\ 3 \div 6 &=& 0 \textrm{, remainder } 3\\ \end{array}$$ One should stop dividing when the quotient found is $0$, and then read the remainders backwards to find the factoradic form. Interestingly, note that the first remainder (upon dividing by $1$) must always be zero -- so all factoradic numbers end in $0$.
In keeping with our earlier remark about the coefficients on the factorials, one should note that as the number we divide by at each step grows without bound. As such, it is possible that some of the remainders encountered will require more than one digit when expressed in base/radix $10$. Placing colons between the remainder values keeps the value of each coefficient/remainder clear.
With all of the above as preface, suppose we seek to build some support for factoradic numbers in Java. Towards this end, write a class Factoradic that will let users of this class perform basic arithmetic on values in factoradic form with ease. To be more precise, construct the Factoradic class so that it has all of the following features:
There should be two constructors -- one that takes an int which is interpreted as the base $10$ value equivalent to the factoriadic to be constructed, and another that takes a String corresponding to its factoradic form (e.g., "3:4:1:0:1:0" in our earlier example).
The class should override the following methods of the Object class:
toString() : This method should return the factoradic form as a Stringequals(Object o) : This method should return true if and only if the objects in question are both instances of the Factoradic class and their values agree.Also include the following instance methods:
base10Value(), which returns an int equal to the value of the Factoradic object in questionplus(Factoradic f), which returns a Factoradic object whose value is the sum of invoking Factoradic object's value and the value of ftimes(Factoradic f), which similarly returns a Factoradic object whose value is the product of the invoking Factoradic object's value and the value of fWhile it causes some duplication of information stored, an efficient strategy from a calculation standpoint will be to keep two instance variables -- one for the value of the Factoradic object, another for the string that represents its factoradic form.
Do not include a main() method in the Factoradic class. Instead, use the class FactoradicTest.java to ensure your Factoradic class is functioning properly.
A sample run of the FactoradicTest class when everything is functioning properly is shown below:
$ java FactoradicTest↵ Testing the Factoradic class... f1 = 3:4:1:0:1:0 = 463 f2 = 1:4:1:1:2:0:0 = 1234 f1 + f2 = 2:2:0:2:2:1:0 = 1697 f1 * f2 = 1:5:1:2:3:0:3:2:0:0 = 571342 f1 == f2 f2 != 2:1:2:0 f1 != "463" Now enter two positive integers a and b separated by a space, and with b>a. After which the values from a to b inclusive will be listed in both base 10 and factoradic form: 100 105↵ 100 = 4:0:2:0:0 101 = 4:0:2:1:0 102 = 4:1:0:0:0 103 = 4:1:0:1:0 104 = 4:1:1:0:0 105 = 4:1:1:1:0