

 |  |
The best case for the quick sort occurs when each partition splits the array into two equal halves. Then, the overall cost for sorting $n$ items is given by:
The partitioning cost for $n$ items, which is $\sim n$ comparisons (and a smaller number of exchanges), and
The cost for recursively sorting two half-size arrays
Since the size of each half is $n/2$, the recurrence relation for the cost function (for comparisons) is closely related to the one governing the merge sort:
$$C(n) = 2 C(\frac{n}{2}) + n \quad ; \quad C(1) = 0$$The result is similar, with the cost function in terms of comparisons for the quicksort also being $O(n \ln n)$.
The worst case for the quick sort occurs when the partition does not split the array (i.e., when one set has no elements at all). Ironically, this happens when the array is sorted!
In this situation, the cost of the sort can be resolved into:
Assuming the "ends-to-the-middle" partitioning technique was used, note that the comparison cost for partitioning a sublist of size $1$ is $0$ and the comparison cost for partitioning a sublist of $n>1$ items is $n+1$ (with a smaller number of exchanges). The latter comes from comparing the first element to the right of the pivot to discover it should be "thrown right", and then comparing $n$ elements with the pivot (including the pivot itself) as we traverse the list backwards from its end, searching for an element to "throw left" (a search which fails).
The cost for recursively sorting the remaining $n-1$ items that are all greater than the pivot and thus to its right. The cost for sorting the zero items to the left of the pivot is of course zero, as is the other base-case cost for sorting a single element. More succinctly, $C(0) = C(1) = 0$.
Thus, the recurrence relation in this case is slightly different:
$$C(n) = C(n-1) + n + 1\quad ; \quad C(1) = 0$$Solving the recurrence relation is straight forward:
$$\begin{array}{rcll} C(n) &=& C(n-1) + (n + 1)& \\\\ &=& [C(n-2) + n] + (n + 1)&\\\\ &=& [C(n-3) + (n-1)] + n + (n + 1)&\\\\ &=& \cdots\\\\ &=& C(1) + 3 + \cdots + (n-2) + (n-1) + n + (n + 1)&\\\\ &=& 0 + 3 + \cdots + (n-2) + (n-1) + n + (n + 1)& \scriptsize{\textrm{now steal $3$ from the $n+1$ to produce a familiar sum}}\\\\ &=& [1 + 2 + 3 + \cdots + (n-2) + (n-1) + n] + (n-2)&\\\\ &=& \displaystyle{\frac{n(n+1)}{2} + (n-2)}&\\\\ &\sim& \displaystyle{\frac{n^2}{2}}&\\\\ \end{array}$$In big-oh notation, the cost in this worst case is then $O(n^2)$.
Since the worst cases occurs when the array is ordered (or highly ordered), we can give ourselves a probabilistic guarantee that this doesn't happen by purposefully shuffling the elements of the array before using the quick sort algorithm. This comes at a slight extra cost, but is worth it to minimize to the point of negligibility the possibility of a $O(n^2)$ cost.
To derive the average number of comparisons needed to quicksort an array of $n$ distinct keys, consider the following:
First, let us denote this average cost by $C_n$ instead of the more traditional $C(n)$. This will help us visually parse the next few expressions without getting lost in a bunch of nested parentheses.
Now, we again consider the cost due to partitioning versus the recursive cost:
The number of comparisons needed to partition (with the "ends-to-the-middle" technique) these $n$ distinct elements is again $(n+1)$.
As for the recursive cost, we start by considering the base case: sorting an empty list or a list of one element requires no comparisons. Thus, $C(0) = C(1) = 0$.
Beyond the base case, however, the recursive cost of both sorting the elements smaller than the pivot and sorting the elements larger than the pivot varies, depending on where the pivot gets placed. Let us denote the positions it could take by $k=0,1,2,\ldots n-1$. If placed at $k=0$, the recursive cost will be $C_0 + C_{n-1}$, as seen in the worst case analysis above. If placed at $k=1$, the recursive cost will be $C_1 + C_{n-2}$ instead. In general, if the pivot is placed at $k$, we have a recursive cost of $C_k + C_{n-k}$.
Each of these $n$ possibilities is equally likely, leading to the average recursive cost of $$\frac{(C_0 + C_{n-1}) + (C_1 + C_{n-2}) + \cdots + (C_{n-1} + C_0)}{n}$$
Note, each $C_k$ for $k=0,1,2,\ldots,n-1$ appears twice in the above expression, allowing us to simplify things a bit...
$$\frac{2(C_0 + C_1 + C_2 + \cdots + C_{n-1})}{n}$$As such, we have a recurrence relation defined by $C_0 = C_1 = 0$ and for $n \ge 2$: $$C_n = (n+1) + \frac{2(C_0 + C_1 + C_2 + \cdots + C_{n-1})}{n}$$ Let's clear the fractions by multiplying by $n$: $$n C_n = n(n+1) + 2(C_0 + C_1 + \cdots + C_{n-2} + C_{n-1})$$ We can eliminate the great majority of $C_k$ terms in the above by observing what this recurrence implies about $C_{n-1}$: $$(n-1) C_{n-1} = (n-1)n + 2(C_0 + C_1 + \cdots + C_{n-2})$$ Seeing the great overlap in terms seen in these last two equations, let us subtract one from the other: $$n C_n - (n-1) C_{n-1} = 2n + 2 C_{n-1}$$ Now comes the interesting part. Note that we can rearrange the terms and divide by $n(n+1)$ to obtain $$\frac{C_n}{n+1} = \frac{C_{n-1}}{n} + \frac{2}{n+1}$$ Look at the first term on the right side. Do you see how structurely it is identical to the first term on the left -- a cost for $k$ elements divided by $(k+1)$. This gives us the ability to make multiple substitutions until we arrive at the base case:
$$\begin{array}{rcl} \displaystyle{\frac{C_n}{n+1}} &=& \displaystyle{\frac{C_{n-1}}{n} + \frac{2}{n+1}}\\\\ &=& \displaystyle{\left[\frac{C_{n-2}}{n-1} + \frac{2}{n}\right] + \frac{2}{n+1}}\\\\ &=& \displaystyle{\left[ \left[ \frac{C_{n-3}}{n-2} + \frac{2}{n-1} \right] + \frac{2}{n}\right] + \frac{2}{n+1}}\\\\ &\cdots&\\\\ &=& \displaystyle{\frac{C_1}{2} + \frac{2}{3} + \frac{2}{4} + \frac{2}{5} + \cdots + \frac{2}{n+1}} \end{array}$$ Recalling that $C_1 = 0$, and then multiplying both sides by $(n+1)$, we find $$C_n = 2(n+1) \left(\frac{1}{3} + \frac{1}{4} + \frac{1}{5} + \cdots + \frac{1}{n+1} \right)$$Notice the right-most factor $(1/3+1/4+1/5+\cdots+1/(n+1))$ can be approximated by the area under the curve $y = 1/x$, as the image below suggests (for $n=7$).
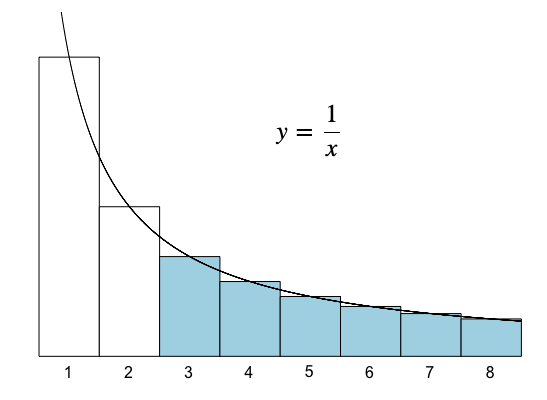
Finding such areas is routine in calculus, resulting in the following here: $$\begin{array}{rcll} C_n &\sim& \displaystyle{2(n+1) \int_3^{n+1} \frac{1}{x}\,dx}&\\\\ &\sim& 2(n+1) \ln n&\\\\ &\approx& 1.39 n \log_2 n& \scriptsize{\textrm{recalling the change of base theorem and observing that } 2 \ln 2 \approx 1.39} \end{array}$$
Thus, on average the quick sort results in a number of comparisons that is roughly $\sim 1.39 n \log_2 n$.
That means one has about $39$ percent more comparisons than merge sort. However, quick sort is faster than merge sort in practice, because there is less data movement during the sort.
We've already mentioned above that initially shuffling the array helps protect us from the worst-case comparison cost. We can additionally improve on the quick sort algorithm with a few other modifications:
Quick sort has a high recursive overhead when the arrays being considered are tiny. In the process of recursively calling quick sort on smaller and smaller arrays -- when the arrays are around 10 elements long, we could switch to an insertion sort to improve the overall efficiency. Alternatively, we could leave the sub-arrays that are around 10 elements long or shorter completely untouched by quick sort, and finish with an insertion sort in one big pass at the end.
The basic quick sort uses the first (or the last) element as the pivot value. The best choice for the pivot would be the median of the array -- but we can't find the median without sorting the array first -- which "puts the cart before the horse" in a certain sense. What we can do, however, is generate a reasonable approximation of the overall median by taking the median of the first, last, and center elements. If we then swap this element to the front of the list in question, we improve the overall efficient of the algorithm by a fair degree.