

 |  |
 Suppose one designs a binary search tree to hold the names of runners in a race using the times they took to the run the race as keys. Certainly the winner of the race has the minimum time, which is easy to find -- but what about the person that came in 10th, or 43rd? Is there a way to efficiently retrieve the name associated with a particular ranking (without having to traverse the entire tree)? On the flip side, given a time known to be in the collection, is there a way to find the rank associated with that time?
Suppose one designs a binary search tree to hold the names of runners in a race using the times they took to the run the race as keys. Certainly the winner of the race has the minimum time, which is easy to find -- but what about the person that came in 10th, or 43rd? Is there a way to efficiently retrieve the name associated with a particular ranking (without having to traverse the entire tree)? On the flip side, given a time known to be in the collection, is there a way to find the rank associated with that time?
As it turns out, there is a way to make such operations extremely fast, although it comes at the cost of adding an instance variable to our Node class. Why, you ask?
Let us adopt the convention that the minimum key has rank $0$, the next smallest has rank $1$, and so on. In doing so, we make the rank of a key $k$ equal to the number of keys in the tree less than $k$.
Now think about the rank of a key $X$, known to be somewhere in the following tree.
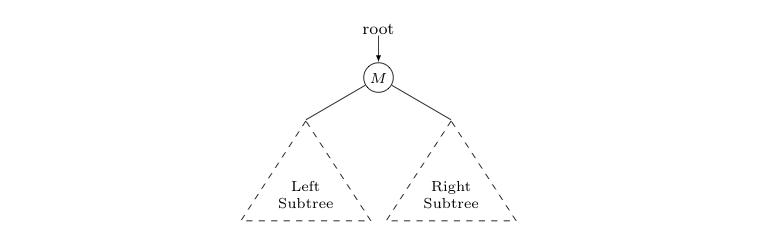
As $X \gt M$, it must be in the right subtree. Consequently, we know a whole bunch of keys that are smaller than $X$ -- namely, $M$ and every node in the left subtree. As such, if we can find the number of keys in the left subtree (plus one more for node $M$), we'll just have to add to that total and the number of additional keys in the right subtree that are less than $X$, to find the rank of $X$.
However, the number of keys in the right subtree that are less than $X$ is precisely the rank of $X$ in this right subtree! With this being a smaller tree, we thus have the potential to find the rank of $X$ recursively. What remains unknown, however, is the keys/nodes of the left subtree previously mentioned.
Think for a moment about how you might find the number of nodes in a given subtree. Would you initialize a counter and traverse the tree? How efficient would that be?
What if instead, we could just "look up" the size for a given subtree somewhere? Of course, there are many possible subtrees, and knowing the size of several of these may be required as we recurse to smaller and smaller trees in our rank calculation.
Recall, every subtree can be identified by the node at which it is "rooted" (i.e., its top-most node). What if we stored the size of the subtree rooted at some node $n$ in the node $n$ itself? That would make for easy and extrememly fast access to this information as we recurse on smaller and smaller subtrees!
The only real cost would be that we would need to keep this subtree size information current as different things happened to the overally tree (e.g., insertion, deletion, etc.).
As such, we add a count instance variable to our inner Node class that will maintain the number of keys/nodes in the subtree rooted at the node in question.
public class BST<Key extends Comparable<Key>, Value>{
private class Node {
private Key key;
private Value val;
private Node left;
private Node right;
private int count; // <-- gives number of nodes in subtree
// topped by this node.
public Node(Key key, Value val) {
this.key = key;
this.val = val;
}
}
private Node root;
...
}
At least in terms of computing the rank of a key -- although perhaps in other contexts as well -- we will want to be able to get this value for any node. However, so that we don't expose the Node class, we make a private "getter" method:
private int size(Node n) {
if (n == null) return 0; // empty trees have 0 nodes, of course
return n.count; // otherwise, we grab the count value for this node
}
With the above method in place, providing a public size() method that returns the number of keys in the entire binary search tree is now "low-hanging fruit", so let's be nice to our client and define the following as well.
public int size() {
return size(root);
}
Now we'll need to go through the methods we have created for binary search trees thus far, and determine if any change the counts associated with any subtrees. At this point, only the put() method does so -- increasing the counts for some (but not all) subtrees.
There are two places in put where we'll need to address node counts. The first is when a new leaf node is created (its count must be initialized to $1$). The second is as we work our way back up the tree (as the smaller recursive steps complete). After each such step, we "correct" the node count to what it should be. Of course for the subtree topped with node $n$, this number of nodes in that subtree can be found by summing the number of nodes in its left and right subtrees, and then adding one more for node $n$ itself. As such, we have the following new version of put():
private Node put(Node n, Key key, Value val) {
if (n == null) {
Node newNode = new Node(key, val);
newNode.count = 1; // leaf nodes should have counts of 1
return newNode;
}
int cmp = key.compareTo(n.key);
if (cmp < 0) // key < n.key
n.left = put(n.left, key, val);
else if (cmp > 0) // key > n.key
n.right = put(n.right, key, val);
else // key == n.key (overwrite)
n.val = val;
n.count = 1 + size(n.left)+ size(n.right); // here, we "fix" n.count,
// lest the "putting" messed it up
return n;
}
Now, finding the rank recursively is both fast and easy! We've already discussed the toughest case -- when the key $k$, whose rank is sought, is greater than the top-most node $n$. If $k \lt n$ instead, than neither $n$, nor any of the keys in the right subtree of $n$ will be counted in the rank. Thus, we can reduce the problem to finding the rank of $k$ in the left subtree.
As the last possibility we need to consider (other than the trivial case of an empty tree) -- if $k$ agrees with the top-most node $n$, then the nodes we count towards the rank are precisely the nodes of the left subtree of $n$. As such, we return the size of $n$'s left subtree in this base case.
Here's the code (appropriately split into two methods: a private recursive one, and a public one that uses the recursive method -- so that the Node class isn't exposed):
public int rank(Key key) {
return rank(key, root);
}
private int rank(Key key, Node n) {
if (n == null)
return 0; // base case: tree is empty
int cmp = key.compareTo(n.key);
if (cmp < 0) // key < n.key
return rank(key, n.left);
else if (cmp > 0) // key > n.key
return 1 + size(n.left) + rank(key, n.right);
else // base case: key == n.key
return size(n.left);
}
Conveniently, this process can be reversed to provide a method that finds a key of a given rank. Suppose you are at the root and someone asks for the key of rank $r$, where $r$ just happened to be the size of the root's left subtree. How would you find the key? It must be the root's key, of course!
Further, had you been asked to find a key with a smaller rank, you would know it was in the left subtree -- and if asked to find a key with a larger rank, you would know it was in the right subtree. Upon realizing this, we just need to tweak the rank sought as we recurse down to smaller subtrees. See if you can follow the code below:
public Key keyWithRank(int rank) {
if (rank < 0) // negative ranks don't make sense
return null;
if (rank > size()) // ranks larger than the number of nodes
return null; // don't make sense either
Node n = keyWithRank(root, rank);
return n.key;
}
private Node keyWithRank(Node n, int rank) {
if (n == null) // if the subtree is empty, we
return null; // can't return anything
int numToLeft = size(n.left);
if (numToLeft > rank) // we are too far to the right...
return keyWithRank(n.left, rank); // so search left for the same rank
else if (numToLeft < rank) // we are too far left...
return keyWithRank(n.right, rank - numToLeft - 1); // so search right, for a rank
// that reflects number left
// we no longer have to count
else // numToLeft == rank,
return n; // so we found it!
}