

 |  |
There is a way simple and effective technique for determining, at least approximately, the nature of the running-time cost function for a given algorithm called a doubling-time experiment.
To illustrate the technique with a concrete example, suppose we wish to express the running-time cost function using Tilde notation for the primitive operation marked in the code below:
int count = 0;
for (int i=0; i < n; i++)
for (int j=i; j < i*i; j++)
if (j%i == 0) {
for (int k=0; k < j; k++)
count++; // <-- primitive operation of interest
}
Note that by its construction, the value count after execution of the above code must agree with the value of $C(n)$. Had we been interested in some other primitive operation, we could have easily added a int count=0; statement right before the code we wished to analyze, and then added another statement, similar to what we currently have, that would increment this counter variable immediately after the primitive operation of interest.
We wish to consider the values of $C(n)$ for a sequence of $n$ values, where each $n$ value in the sequence is double the previous $n$ value. Adding a statement to print the value of our counter variable, count, at the bottom of the code above lets us generate the following $C(n)$ values quickly:
| $n$ | $C(n)$ | $\displaystyle{\frac{C(2n)}{C(n)}}$ |
|---|---|---|
| 4 | 11 | 29.27 |
| 8 | 322 | 20.43 |
| 16 | 6580 | 17.90 |
| 32 | 117800 | 16.89 |
| 64 | 1989456 | 16.43 |
| 128 | 32686752 | 16.21 |
| 256 | 529904960 | $\vdots$ |
Note how the values appear to be leveling off near $16$. This is of course, exactly what one would expect if $C(n) \sim k \cdot n^4$ for some constant $k$. To see why, consider the following calculation:
$$\textrm{For large } n, \quad \frac{C(2n)}{C(n)} \approx \frac{k \cdot (2n)^4}{k \cdot n^4} = 2^4 = 16$$Different values of this limiting ratio for $C(2n)/C(n)$ suggest different types of cost functions. The table below summarizes some of the more common associations:
| Value of Limiting Ratio | Consistent with a cost function |
|---|---|
| $1$ | Constant or Logarithmic |
| $2$ | Linear or Linearithmic |
| $4$ | Quadratic |
| $8$ | Cubic |
| $2^b$ for $b \gt 3$ | $b^{th}$-degree Polynomial |
The above method for making an educated guess about the nature of a cost function $C(n)$ proves valuable in many contexts, and given how easy it is to implement should strongly be considered as a first step in the running-time analysis of any algorithm whose cost function appears difficult to find.
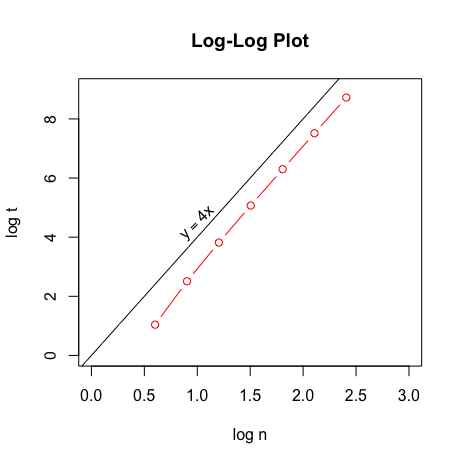
Another technique to reveal the nature of the underlying cost function is to create a log-log plot of ordered pairs $(\log n, \log t)$ where $n$ is the problem size and $t$ is the running time. For a sufficient number of these pairs, seeing the resulting scatter plot be roughly linear with slope $m \gt 1$ is consistent with the cost function being $\sim k \cdot n^m$, for some constant $k$.
Below is the log-log plot for the running times calculated in the example above. The line $y=4x$, is shown as well so that one can compare the slopes. Seeing the slope of the red curve approach 4 as one moves to the right suggests again that $C(n) \sim k \cdot n^4$ for some constant $k$.
So we have two quick calculations telling us that the cost function for the code in our example is likely a fourth degree polynomial. Let us see if we can find $C(n)$ exactly..
Here is the code again, for easy reference:
int count = 0;
for (int i=0; i < n; i++)
for (int j=i; j < i*i; j++)
if (j%i == 0) {
for (int k=0; k < j; k++)
count++; // <-- primitive operation of interest
}
Consider the values of $j$ for which the body of the middle for-loop executes for the first few values of $i$:
$$\begin{array}{rcl}
i = 0 &\rightarrow& \textrm{(none)}\\
i = 1 &\rightarrow& \textrm{(none)}\\
i = 2 &\rightarrow& \fbox{2}, 3\\
i = 3 &\rightarrow& \fbox{3},4,5,\fbox{6},7,8\\
i = 4 &\rightarrow& \fbox{4},5,6,7,\fbox{8},9,10,11,\fbox{12},13,14,15\\
\end{array}$$
The "boxed" values above are those for which the conditional j%i == 0 is true. Conveniently, for each one of these boxed $j$ values, the inner-most loop executes the primitive function the same number of times as appears in the box. Thus, we can find $C(n)$ with a sum that begins with the following terms:
Factoring out the common factors in each parenthesized group we can rewrite this in the following form:
$$2(1) + 3(1+2) + 4(1+2+3) + \cdots + (n-1)(1+2+3+\cdots+(n-2))$$More compactly, we can express $C(n)$ as
$$\sum_{i=2}^{n-1} i \cdot (1+2+3+\cdots+(i-1))$$The sum $(1 + 2 + 3 + \cdots + (i-1))$, one should recognize. This is just $i(i-1)/2$. Making this substitution, we have
$$C(n) = \sum_{i=2}^{n-1} \frac{i^2(i-1)}{2}$$Noting that for $i=0,1$ the corresponding term inside the sum would be zero, we can start the sum at $i=0$ without affecting anything. We can additionally expand and then separate the term inside the sum to obtain
$$C(n) = \sum_{i=0}^{n-1} \left(\frac{i^3}{2} - \frac{i^2}{2}\right)$$The reason for doing this is to isolate/manufacture the terms $\sum_{i=0}^n i^3$ and $\sum_{i=0}^n i^2$, whose formulas we remember from algebra. Continuing with this strategy, we turn the overall sum into a difference of two simpler summations:
$$C(n) = \frac{1}{2} \left( \sum_{i=0}^{n-1} i^3 - \sum_{i=0}^{n-1} i^2 \right)$$Finally, we add the terms corresponding to $i=n$ in both sums, only to subtract them right off again...
$$C(n) = \frac{1}{2} \left( \left[ \sum_{i=0}^n i^3 \right] - \left[ \sum_{i=0}^n i^2 \right] - n^3 + n^2\right)$$Now -- as was our strategy -- we use the well-known formulas from algebra:
$$\sum_{i=0}^n i^3 = \frac{n^2(n+1)^2}{4} \quad \textrm{ and } \quad \sum_{i=0}^n i^2 = \frac{n(n+1)(2n+1)}{6}$$to find a closed-form formula for $C(n)$:
$$C(n) = \frac{1}{2} \left( \frac{n^2(n+1)^2}{4} - \frac{n(n+1)(2n+1)}{6} - n^3 + n^2 \right)$$Algebraically simplifying things, we can say equivalently
$$C(n) = \frac{n(n-1)(n-2)(3n-1)}{24}$$Whew! That was a lot of work! However, note that when expanded this gives $C(n)$ as a fourth degree polynomial in $n$ -- which is perfectly consistent with our "guess" that $C(n) \sim k \cdot n^4$ for some constant $k$!
The difference in how quickly we came up with the Tilde approximation versus the exact formula for $C(n)$ illustrates why we are often content with using the asymptotic notations. 🙂
There is another take-away here as well. Having some idea of the formulas for certain often-encountered summations and other expressions -- or at least the Tilde approximations for these formulas -- can be extremely handy. To that end, the following sums and expressions are frequently encountered in the running-time analysis of code:
| Sum/Expression | Formula or Approximation |
|---|---|
| $1 + 2 + 3 + 4 + \cdots + n$ | $$\frac{n(n+1)}{2} \quad \sim \quad \frac{n^2}{2}$$ |
| $1^2 + 2^2 + 3^2 + 4^2 + \cdots + n^2$ | $\displaystyle{\frac{n(n+1)(2n+1)}{6} \quad \sim \quad \frac{n^3}{6}}$ |
| $1^3 + 2^3 + 3^3 + 4^3 + \cdots + n^3$ | $\displaystyle{\frac{n^2(n+1)^2}{4} \quad \sim \quad \frac{n^4}{4}}$ |
| $1 + 2 + 4 + 8 + \cdots + 2^m$ | $2^{m+1}-1 \quad \textrm{(if } n=2^m, \textrm{then } \sim 2n)$ |
| $\ln 1 + \ln 2 + \ln 3 + \ln 4 + \cdots + \ln n$ | $\ln n! \sim n\ln n$ |
| ${}_{n}C_{\,k}$ | $\displaystyle{\sim \frac{n^k}{k!}} \, \textrm{ when $k$ is a small constant}$ |
| $(1 - 1/n)^n$ | $\displaystyle{\textrm{close to } \frac{1}{e} \textrm{ for large $n$, so } \sim 1}$ |