

 |  |

Having now covered the basics of trigonometry, let's see how we can put this together with the depressed terms method of solving quadratic equations to solve cubic equations whose roots are all real. As a concrete example, let us consider the following cubic equation: $$x^3 - 2x^2 - 5x + 6 = 0$$ Note that we have $3$ occurences of $x$ in the above. We hope to eliminate $2$ of them, so that we can apply the socks and shoes principle.
Francois Viete (whom we've discussed before) and German mathematician Ehrenfried Walther von Tschirnhaus realized that the method of depressed terms provides the opportunity to eliminate $1$ of these fairly easily.
Suppose that the function $f(x)$ outputs the value of the left side of our equation. Then consider the function $g(x) = f(x+h)$, whose graph is some shift of the graph of $y=f(x)$. As when we applied this method to solving quadratics, note that the graph of $y=g(x)$ is simply a horizontal shift of the graph of $y=f(x)$.

While the sign of $h$ determines whether this shift is to the left or right, should we find any roots to $g(x) = 0$ we can deduce corresponding roots to $f(x)=0$ by simply adding $h$ to each of the found roots to $g(x) = 0$.
Plugging in $(x+h)$ as input to $f$ and expanding the result as quadratic in $x$, we find $$\begin{array}{rcl} g(x) &=& f(x+h)\\ &=& (x+h)^3 - 2(x+h)^2 - 5(x+h) + 6\\ &=& x^3 + 3x^2 h + 3xh^2 + h^3 -2x^2 - 4xh - 2h^2 - 5x - 5h + 6\\ &=& x^3 + (3h-2)x^2 + (3h^2 - 4h - 5)x + (h^3 - 2h^2 - 5h + 6)\\ \end{array}$$ As before, we may find it useful to note that the constant term of $g(x)$ must always be $f(h)$, given the way it was defined.
Note the coefficient on the quadratic term, however. Just as we can depress the linear term in a quadratic to find its solutions, let us here depress the quadratic term for the resulting cubic to solve this problem. That is to say, let us find $h$ so that $(3h-2) = 0$, so that $g(x)$ has no quadratic term.
This of course is almost immediate, as $3h-2 = 0$ implies $h=\frac{2}{3}$
Now, finding the rest of $g(x)$ for this special $h$ value, we have $$\begin{array}{rcl} g(x) &=& x^3 + \left(3 (\frac{2}{3})^2 - 4 (\frac{2}{3}) - 5\right) x + \left((\frac{2}{3})^3 - 2(\frac{2}{3})^2 - 5(\frac{2}{3}) + 6\right)\\ &=& x^3 + \left(\frac{4}{3} - \frac{8}{3} - \frac{15}{3}\right) x + \left( \frac{8}{27} - \frac{24}{27} - \frac{90}{27} + \frac{162}{27}\right)\\ &=& x^3 - \frac{19}{3} x + \frac{56}{27}\\ \end{array}$$ As such, the roots of $f(x) = 0$ can be found by adding $h=\frac{2}{3}$ to each root of $x^3 - \frac{19}{3} x + \frac{56}{27} = 0$. The problem, however, is that this last equation still has more than one occurrence of $x$. This is where trigonometry can help!
Notice that if we solve for the constant in this equation, we get $$-\frac{56}{27} = x^3 - \frac{19}{3}x$$ Now recall the triple-angle formula for the cosine: $$\cos 3\theta = 4\cos^3 \theta - 3\cos \theta$$ Notice the similarities between the two. On their right sides, we have in both situations a cubic and a linear term -- in terms of $x$ for the first, and in terms of $\cos \theta$ for the second.
Our aim is to make these two look even closer in form, and then assume some nice relationship exists between them (i.e., one where we can solve for either in terms of the other), allowing us to make a clever substitution (more on that in a minute).
With this in mind, and noting that there is a coefficient on the $\cos^3 \theta$ term but not on the $x^3$ term, -- let's divide the equation in $\theta$ by $4$ to get $$\frac{\cos 3\theta}{4} = \cos^3 \theta - \frac{3}{4} \cos \theta$$ Now for the clever substitution! Suppose we choose $\theta$ and some real value $a$ so that $x = a\cos \theta$. There are lots of $(a,\theta)$ pairs possible here. To see this, note that when $0 \lt \theta \lt \frac{\pi}{2}$, increasing $\theta$ by a "smidge" will require decreasing $a$ by some amount to keep their product equal to $x$. Similar things happen when $\theta$ is in other ranges.
The many options we have for the particular pair of $\theta$ and $a$ values we will use gives us some flexibility to make some desired thing happen -- just as there were many $h$ we could have used to define $g(x)$, so we picked the one that would make the quadratic term disappear.
Let's consider what happens if $x = a\cos \theta$ and we use this to rewrite our equation currently in terms of $x$ to be in terms of $\cos \theta$: $$-\frac{56}{27} = (a \cos \theta)^3 - \frac{19}{3}(a \cos \theta)$$ Dividing both sides by $a^3$ (to return the coefficient on $\cos^3 \theta$ to $1$, we have $$-\frac{56}{27a^3} = \cos^3 \theta - \frac{19}{3a^2} \cos \theta$$ Recall again the earlier relationship stemming from the triple-angle formula: $$\frac{\cos 3\theta}{4} = \cos^3 \theta - \frac{3}{4} \cos \theta$$ If we can make the right side of our equation look exactly like the right side of the equation immediately above, then we could replace it with $\frac{1}{4} \cos 3\theta$. This would reduce the number of occurrences of our variable down to a single occurrence -- allowing us to solve the rest with the socks and shoes principle. Given this, let us choose the value $a$ to be the one that will make the coefficient on $\cos \theta$ equal to $\frac{3}{4}$.
Finding this $a$, we see that: $$\frac{19}{3a^2} = \frac{3}{4} \quad \longrightarrow \quad a^2 = \frac{19 \cdot 4}{9} \quad \longrightarrow \quad a = \pm \frac{2}{3}\sqrt{19}$$
We should pause for a moment here and consider what could have happened just now had we attacked a slightly different cubic equation. Suppose the $19$ above had been negative. This could easily happen! (Can you make a cubic where it does?) In such a case, the two values associated with the variable $a$ will then be complex. As will be seen in the paragraphs coming, such a situation would require we consider when the cosine of an angle is complex! Certainly this never happens when the input to the cosine is real -- but what if the cosine function (and others) could accept complex-valued inputs? Lest we get ahead of ourselves, let us leave those exciting possibilities linger for now. But don't worry, we'll pick them up again soon!
With two options for $a$ that both accomplish what we seek to do, let us pick the positive one. With $a = \frac{2}{3}\sqrt{19}$, we then have $$ \frac{-56}{27 ( \frac{2}{3} \sqrt{19} )^3} = \cos^3 \theta - \frac{3}{4} \cos \theta $$ Simplifying the left side and then swapping sides (just to make it look prettier), we have $$\cos^3 \theta - \frac{3}{4} \cos \theta = -\frac{7}{19^{3/2}}$$ Finally, we have thus set ourselves up to replace the two occurrences of $\theta$ with a single one -- using the relationship resulting from the triple-angle formula for cosine: $$\frac{\cos 3\theta}{4} = -\frac{7}{19^{3/2}}$$ From here, we use socks and shoes. Of course, we must be careful when navigating the one "wrinkle" that the cosine function is technically not invertible. That said, we know how to find (using the arccosine function, $\cos^{-1}$) all angles for which their cosine equals some given value. $$\begin{array}{rcl} \displaystyle{\frac{\cos 3\theta}{4}} &=& -\displaystyle{\frac{7}{19^{3/2}}}\\\\ \cos 3\theta &=& \displaystyle{-\frac{28}{19^{3/2}}}\\\\ 3\theta &=& \pm \displaystyle{\cos^{-1} \left(\frac{-28}{19^{3/2}}\right)+2\pi n \quad \textrm{where $n$ is an integer}}\\\\ \theta &=& \pm \displaystyle{\frac{1}{3} \cos^{-1} \left(\frac{-28}{19^{3/2}}\right)+\frac{2\pi n}{3} \quad \textrm{where $n$ is an integer}}\\\\ \end{array}$$ Our last steps are to work backwards from this solution for $\theta$, first to a solution $x$ to $g(x)=0$, and then to a solution $x$ to $f(x)=0$.
Recall that we let $x = a \cos \theta$, except now we know the value of $a$ we wanted -- namely, $a = \frac{2}{3}\sqrt{19}$. As such, the following $x$ solves $g(x)=0$: $$x = \frac{2}{3}\sqrt{19} \cos \left(\pm \frac{1}{3} \cos^{-1} \left(\frac{-28}{19^{3/2}}\right)+\frac{2\pi n}{3}\right) \quad \textrm{where $n$ is an integer}$$ All that remains is to add $h=\frac{2}{3}$ to these solutions to find the $x$ values that solve $f(x)=0$ $$x = \frac{2}{3}\sqrt{19} \cos \left(\pm \frac{1}{3} \cos^{-1} \left(\frac{-28}{19^{3/2}}\right)+\frac{2\pi n}{3}\right) + \frac{2}{3}\quad \textrm{where $n$ is an integer}$$ Of course, we probably want to simplify these if we can! Evaluating the above with a calculator for $n=0$, $n=1$, and $n=2$ and the "$+$" option (things start to repeat after that), we shockingly get the below as our solution! $$x = 1, x = -2, \textrm{ or } x = 3$$ Note we can easily verify this, as if true our original polynomial should factor into: $$x^2 - 2x^2 - 5x + 6 = (x-1)(x+2)(x-3)$$ Expanding the right side, we see that this is true. Wow! 😀

Just as we saw multiple ways to solve quadratic equations, there are also mutiple ways to solve cubic equations. Interestingly, some of these give the solutions in a radically different form. While the method above expressed it's solutions in terms of trigonometric functions and their inverses, the method below known as Cardano's method, after Italian mathematician Gerolamo Cardano, will reveal it's solutions in a more algebraic form -- one that involves nested roots of various values. Seeking to give attribution to where it is due, one should note that while Gerolamo Cardano published the method of solution seen below -- it was first discovered by Scipione del Ferro, another Italian mathematician, born in $1465$.
Consider the following cubic equation: $$x^3 + 3x^2 + 4x + 3 = 0$$ We begin in the same manner as the previous method -- we depress the quadratic term in the related cubic function $f(x) = x^3 + 3x^2 + 4x + 3$.
Recall this means defining a new function $g(x) = f(x+h)$, and then writing it as a cubic function of $x$. Thus, $$\begin{array}{rcl} g(x) &=& (x+h)^3 + 3(x+h)^2 + 4(x+h) + 3\\ &=& (x^3 + 3x^2 + 3xh^2 + h^3) + 3(x^2 + 2xh + h^2) + 4(x+h)+3\\ &=& x^3 + (3h+3)x^2 + (3h^2+6h+4)x + (h^3+3h^2+4h+3)\\ \end{array}$$ We wish the coefficient on $x^2$ to be zero, so we choose $h=-1$.
Evaluating the other coefficients above in terms of this $h$ value, we can then write $$g(x) = x^3 + x + 1$$ In this example, the coefficient on $x$ and the constant term worked out nicely. They need not always do so. In these other cases, the coming arithmetic will be tedius -- so let us merely say that after depressing the quadratic term, we will always see a function $g$ in the following form for some real values $m$ and $n$ (for the example here discussed, $m=1$ and $n=1$): $$x^3 + mx + n = 0$$
Much like the previous solution of a cube used the triple-angle formula for cosine as a trick to reduce the now two occurrences of $x$ down to a single occurrence of an unknown variable -- we seek the same goal, but use a different trick to get there.
Recalling the cube of a binomial: $(a+b)^3 = a^3 + 3a^2b + 3ab^2 + b^3$, rearrange the terms to discover the following: $$\underbrace{(a+b)^3}_{\textrm{a cubic term}} - 3ab\underbrace{(a+b)}_{\textrm{a linear term}} - (a^3 + b^3) = 0$$ Here's the trick: Noting the similarity in form between our depressed cubic and the equation immediately above, let us equate the following: $$\begin{array}{rcl} m &=& -3ab\\ n &=& -(a^3+b^3) \end{array}$$ and let $x=a+b$, so that $x$ solves both $$x^3 + mx + n = 0$$ and $$x^3 - (3ab)x - (a^3 + b^3) = 0$$ Then, we simply solve for $a$ and $b$ in terms of $m$ and $n$ and add them together to find $x$, a solution to the depressed cubic whose roots we seek.
To solve this system, it will be easier to only see the same powers of $a$ and $b$, so we cube both sides of the first equation. This gives us the system: $$\begin{array}{rcl} m^3 &=& -27a^3 b^3\\ n &=& -(a^3+b^3) \end{array}$$ Now let us hide the detail of the cubing, so we can better see the structure of what is left, by letting $A = a^3$ and $B = b^3$: $$\begin{array}{rcl} m^3 &=& -27 A B\\ n &=& -(A + B) \end{array}$$ Now, it is clear that $$\begin{array}{rcl} A B &=& \displaystyle{-\frac{m^3}{27}}\\ A + B &=& -n \end{array}$$ As seen below, solving for $B$ in the first and substituting the result into the second reveals an equation easily convertible into a quadratic in $A$! $$A B = -\frac{m^3}{27} \quad \longrightarrow \quad B = -\frac{m^3}{27A}$$ Then, $$\begin{array}{rcl} A - \frac{m^3}{27A} &=& -n\\ 27A^2 - m^3 &=& -27nA \quad \quad {\scriptsize \textrm{(after multiplying both sides by $27A$ to eliminate the fractions)}}\\ 27 A^2 + 27n A - m^3 &=& 0 \end{array}$$ This quadratic in $A$ can be quickly solved with the quadratic formula: $$A = \frac{-27n \pm \sqrt{(27n)^2 - 4(27)(-m^3)}}{2\cdot 27}$$ Just as a bit of flourish, we can rewrite the above with a bit more symmetry (allowing us to remember it more easily, if that be desired). The algebra to convert the above form to the one given below is straight-forward and not too long (so the reader should try their hand at doing so!) $$A = -\frac{n}{2} \pm \sqrt{\left(\frac{n}{2}\right)^2 + \left(\frac{m}{3}\right)^3}$$ By symetry one of these will be the solution for $A$, and the other will be a solution for $B$. Given that $a = \sqrt[3]{A}$, $b = \sqrt[3]{B}$, and one solution sought will be given by $x = a + b$, we have $$x = \sqrt[3]{-\frac{n}{2} + \sqrt{\left(\frac{n}{2}\right)^2 + \left(\frac{m}{3}\right)^3}} + \sqrt[3]{-\frac{n}{2} - \sqrt{\left(\frac{n}{2}\right)^2 + \left(\frac{m}{3}\right)^3}}$$ Recalling that in our particular depressed cubic $g(x) = x^3 + mx + n$ both $m$ and $n$ equaled $1$, we now have one solution in hand to $g(x) = 0$: $$x = \sqrt[3]{-\frac{1}{2} + \sqrt{\frac{1}{4} + \frac{1}{27}}} + \sqrt[3]{-\frac{1}{2} - \sqrt{\frac{1}{4} + \frac{1}{27}}}$$ Finally, adding $h=-1$ to the above solution to $g(x) = 0$ shifts it to a solution of $f(x) = 0$, our original cubic equation $x^3 + 3x^2 + 4x + 3 = 0$: $$x = \sqrt[3]{-\frac{1}{2} + \sqrt{\frac{1}{4} + \frac{1}{27}}} + \sqrt[3]{-\frac{1}{2} - \sqrt{\frac{1}{4} + \frac{1}{27}}} - 1 \approx -1.682327804$$ One will note that an approximation to the exact solution has been provided above. While finding the other two roots will be relatively simple from here -- the arithmetic involved can be ...well, awful! As such, we will use approximations from this point forward, but will provide enough detail to allow the ambitious (masochistic?) reader to find the other roots exactly, if they so desire.
Armed with the knowledge that $r_1 \approx -1.682327804$ is a root to $f(x) = 0$, by the factor theorem we know $f(x)$ has a factor of $(x-r_1)$. Dividing $f(x)$ by this factor produces a quadratic whose roots (let us call them $r_2$ and $r_3$) provide the remaining two solutions to $f(x) = 0$. These of course, can be found via the quadratic formula.
In this case, doing that division yields the additional (complex) roots $r_2$ and $r_3$: $-0.658836 \pm 1.16154i$. As a double-check, plugging these roots into $f(x)$, we find $f(r_2) = f(r_3) \approx 3.06404 \times 10^{-6} + 4.0109 \times 10^{-6} i$, which is quite close to zero indeed!
Just as we can apply "completing the square", "Po-Shen Loh's method", or "the method of depressed terms" to a general quadratic equation $ax^2 + bx + c = 0$ to arrive at the quadratic formula, you could also apply Cardano's method (or others) to the general cubic equation $ax^3+bx^2+cx+d=0$ to find its three roots.
Should you be interested enough to do so, you would get the following:
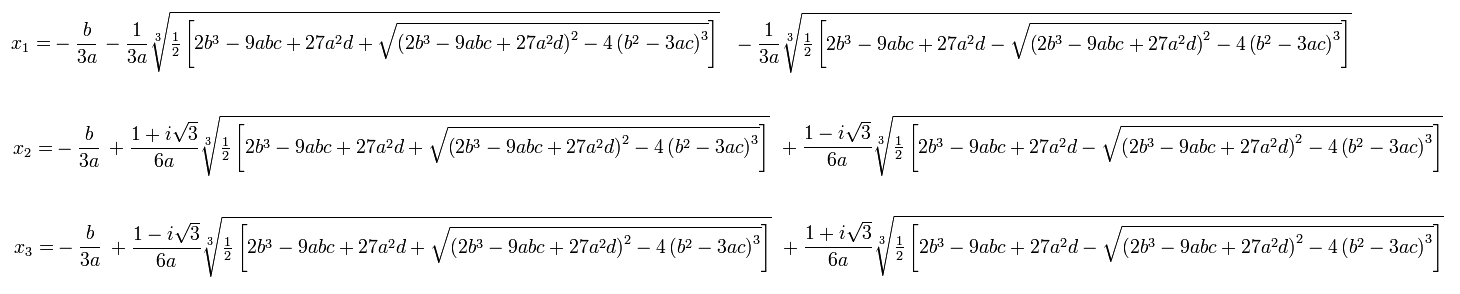
While many have the quadratic formula memorized -- for obvious reasons, one probably doesn't want to try to commit the above to memory! Still, it is very cool that a general solution exists! Makes one wonder about a quartic (i.e., fourth-degree) equation, doesn't it?