

 |  |
Treating each function as a composition of the simple functions we have discussed (i.e., vertical translations, scalings, reflections, absolute value, reciprocals, even and odd powers, even and odd roots, exponentials, and logarithms), find the graph of the function by applying the appropriate transformations to an appropriate starting graph. Show all intermediate functions/graphs that result, in the order these transformations have been applied. Your graphs should indicate the coordinates of all interesting points (i.e., intercepts, or points that were intercepts at some intermediate stage as the aforementioned transformations were applied), either through labeling the points with ordered pairs, or by adding tick marks on your axes specifically for these points. If these interesting points are not sufficient to establish the “scale” of the graph, one should add coordinates or tick marks for at least one more point to make this clear.
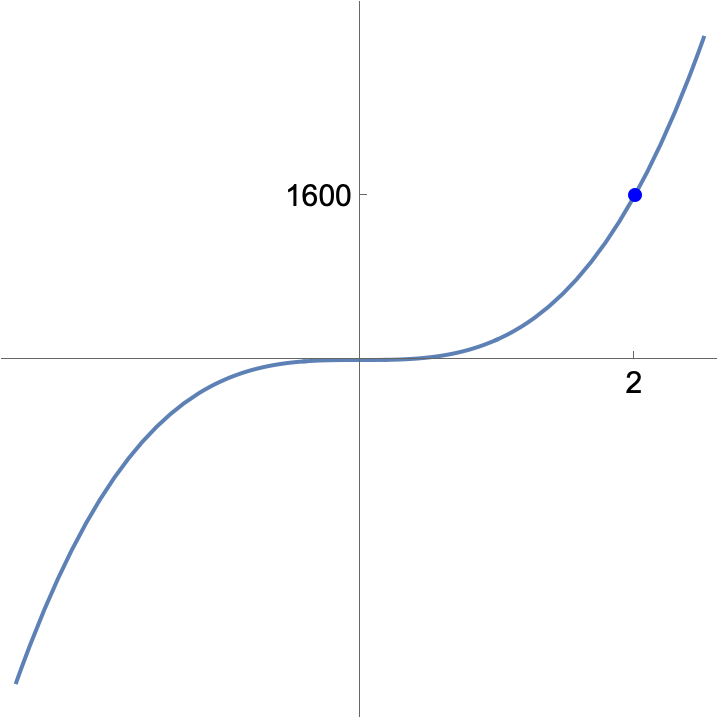
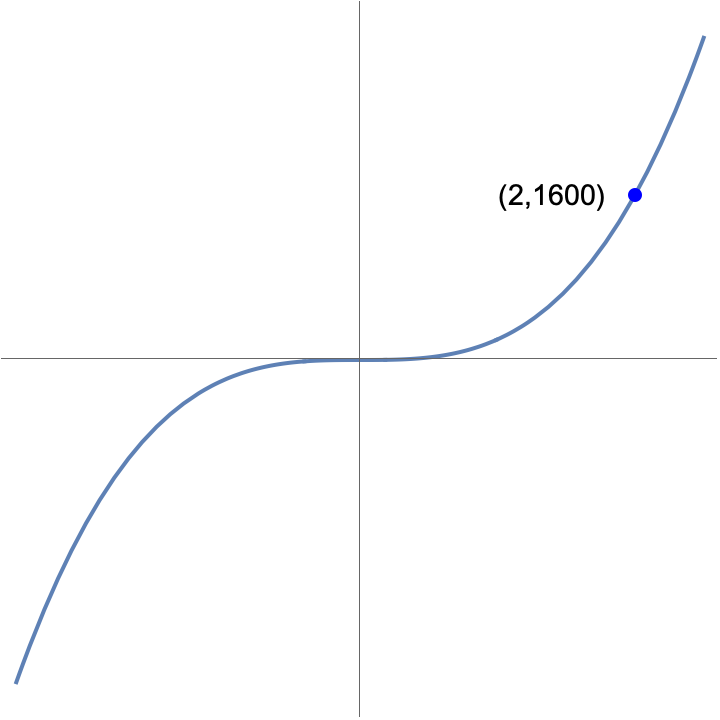
With regard to this last point of establishing scale -- consider the function $f(x) = 200x^3$. There is a single "interesting point" (an intercept) at $(0,0)$. However – with no other points labeled (or tick marks on the axes shown), it is not clear what the scale is for the two axes. Having some indication of this scale is important as it gives us a rough idea for some given x, just how big its associated y value will be.
Note: we don’t want to have to draw our graphs so that a unit on the x-axis is equal in length to a unit on the y-axis, as the magnitudes of the x and y coordinates often differ substantially.
We should thus label at least one other point to give some indication of the magnitudes involved. As possibilities, any of the following would be fine: $(1,200)$, $(2,1600)$, $(−1,−200)$, $(−3,−5400)$. Others could work as well, as long as they are on the graph of the function.
Alternatively, we could indicate the scale by adding for whatever point chosen some tick marks on the two axes to indicate its position. An example with two tick marks included and another with coordinates is shown below:
$\displaystyle{f(x)=|4^{x-1}+3|}$
$\displaystyle{f(x)=\log _5\left(\frac{-|x|}{5}+4\right)}$
$\displaystyle{f(x)=\frac{1}{4 | x| }-2}$
$\displaystyle{f(x)=\left| \log _4\left(-\frac{x}{5}\right)\right|}$
$\displaystyle{f(x)=-\frac{| x| ^2}{9}}$
$\displaystyle{f(x)=\frac{1}{3 | x| -1}}$
$\displaystyle{f(x)=\left(-\frac{x}{4}-3\right)^2}$
$\displaystyle{f(x)=5 | -x-1| ^4}$
$\displaystyle{f(x)=-4^{5 x+4}}$
$\displaystyle{f(x)=4 \left(\log _3(-| x| )+4\right)}$
$\displaystyle{f(x)=5-\sqrt[3]{| x| }}$
$\displaystyle{f(x)=-\frac{1}{| x| }-5}$
$\displaystyle{f(x)=\frac{1}{-| x| -4}}$
$\displaystyle{f(x)=| 2-5 x| ^2}$
$\displaystyle{f(x)=\frac{| x-2| ^4}{5}}$
$\displaystyle{f(x)=-2 \log _6(| x| )-3}$
$\displaystyle{f(x)=\frac{| 2-x| ^5}{32}}$
$\displaystyle{f(x)=-\frac{| x-5| ^5}{32}}$
Treating each function as a composition of the simple functions we have discussed (i.e., vertical translations, scalings, reflections, absolute value, reciprocals, even and odd powers, even and odd roots, exponentials, and logarithms), find the graph of the function by applying the appropriate transformations to an appropriate starting graph.
$\displaystyle{f(x)=\frac{1}{5} \left(-\frac{1}{x}-2\right)}$
$\displaystyle{f(x)=-5 \left| \sqrt[6]{x}\right| -3}$
$\displaystyle{f(x)=-| x| ^2-5}$
$\displaystyle{f(x)=\frac{1}{5} \left(2-2^{| x| }\right)}$
$\displaystyle{f(x)=\frac{1}{5} \left(| x| ^5+4\right)}$
$\displaystyle{f(x)=\left| 4-\frac{x}{2}\right| ^2}$
$\displaystyle{f(x)=\left| -\sqrt{2} \sqrt[4]{x}-3\right|}$
$\displaystyle{f(x)=-\frac{| x| ^5}{32}}$
$\displaystyle{f(x)=-\left| \sqrt[5]{5 x+4}\right|}$
$\displaystyle{f(x)=-| 2 x+1| ^3}$
$\displaystyle{f(x)=|2^{-x}-3|}$
$\displaystyle{f(x)=\sqrt[7]{| x| }-5}$
$\displaystyle{f(x)=3 | x| ^3+4}$
$\displaystyle{f(x)=3 |\left(3-3^{x}\right)|}$
$\displaystyle{f(x)=-\log _2(5 x)-2}$
$\displaystyle{f(x)=\frac{\sqrt[5]{2-| x| }}{3}}$
$\displaystyle{f(x)=3 (-| x| -2)^5}$
$\displaystyle{f(x)=-\left(\frac{x}{4}+5\right)^4}$
$\displaystyle{f(x)=-5^{| x| +1}}$
$\displaystyle{f(x)=5-\frac{\log _2(| x| )}{3}}$
$\displaystyle{f(x)=\frac{1}{4 | x| }}$
$\displaystyle{f(x)=-5 3^{| x| -5}}$
$\displaystyle{f(x)=2 \left(| x| ^5-5\right)}$
$\displaystyle{f(x)=| x+3| ^2}$
$\displaystyle{f(x)=-5 | x-3| ^4}$
$\displaystyle{f(x)=-2^{x/4}-3}$
$\displaystyle{f(x)=-\frac{1}{5} \left| \log _7(x)\right| -3}$
$\displaystyle{f(x)=-3 \left| \sqrt[5]{x}\right| -1}$
$\displaystyle{f(x)=-3 | x+3| ^5}$
$\displaystyle{f(x)=-\left| \sqrt[6]{x}-5\right|}$
$\displaystyle{f(x)=\sqrt[3]{3} \sqrt[3]{| x| }}$
$\displaystyle{f(x)=-\frac{1}{5 x}-1}$
Graphs for functions #1-16 in this problem
Note: Graphs for the remaining functions can be quickly obtained using Desmos, if desired. Follow the link just given to pull up the Desmos online graphing calculator, and then enter the function whose graph is desired in the blank on the resulting page labeled "1". The graph of the function is automatically drawn in the right pane on that page.