

 |  |
Given the braids on $5$ strands $B_1 = x_2^2 x_3^{-1} x_1 x_1^{-1} x_4^{-3}$ and $B_2 = x_1 x_2 x_1 x_4^2$, answer the following questions:
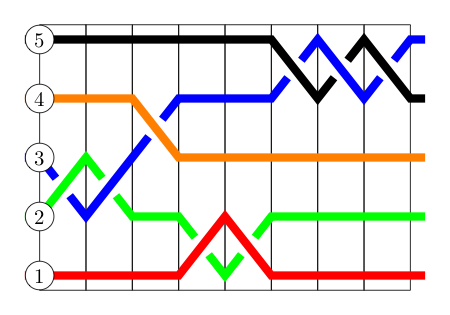
Draw the braid $B_1$. (Make sure you see the exponents on the first and last elementary braids involved.)
Write the braid word for the concatenation $B_1 * B_2$.
Apply Artin's relation to $B_2$ to produce a braid word for an equivalent braid.
To which of the following two braids is $B_1$ equivalent? $$B_3 = x_2 x_3^{-1} x_2 x_1 x_1^{-1} x_4^{-3} \quad \quad B_4 = x_2^2 x_3^{-1} x_4^{-3}$$
Is $(B_1 * B_2) * B_2 = B_1 * (B_2 * B_2)$? How do you know?
Remember, when we see $x_i$, that indicates a crossing of the $i^{th}$ and $(i+1)^{th}$ strands, where the ascending strand is on top. $x_i^{-1}$ represents a crossing between the same strands, but with the descending strand on top. As such, $B_1$ would look like the following:
Concatenation in this context just means adjoining braid $B_2$ to the end of $B_1$ (just as all the elementary braids that comprise both are adjoined together. As such, we get the braid word $B_1 * B_2 = x_2^2 x_3^{-1} x_1 x_1^{-1} x_4^{-3} x_1 x_2 x_1 x_4^2$
Recall Artin's relation is $x_i x_{i+1} x_i = x_{i+1} x_i x_{i+1}$. We see the pattern on the left in the first three elementary braids of $B_2$. As such, we replace $x_1 x_2 x_1$ with $x_2 x_1 x_2$ to get $x_2 x_1 x_2 x_4^2$
$B_1$ is not equivalent to $B_3$ as $x_2$ and $x_3^{-1}$ don't commute as they are not distant braids (i.e., $|2-3| < 2$). However, $B_1$ is equivalent to $B_4$ as $x_1 x_1^{-1}$ can be collapsed to the identity braid $I$, and then removed given the properties of inverses and what it means to be the identity.
Yes, braid concatenation is associative. A similar statement could be made for any three braids, not just $B_1$, $B_2$, and $B_2$ as seen here.
Consider the following permutations, and then answer the questions that follow: $$p_1 = \left[ \begin{array}{cccccccc} 1 & 2 & 3 & 4 & 5 & 6 & 7\\ 5 & 7 & 6 & 1 & 4 & 2 & 3 \end{array} \right] \hspace{1cm} p_2 = \left[ \begin{array}{cccccccc} 1 & 2 & 3 & 4 & 5 & 6 & 7\\ 2 & 4 & 3 & 7 & 1 & 6 & 5 \end{array} \right]$$ $$ p_3 = (1,2,6,4,7) \hspace{1cm} p_4 = (3,5) \hspace{1cm} p_5 = (1,3,4,7)(2,6) $$
Find the composition $p_1 \cdot p_2$. (Express your answer using the bracket notation.)
Convert $p_1$ to cycle notation.
Find the composition $p_3^{2} \cdot p_4 \cdot p_5^{-1}$. (Express your answer using cycle notation.)
Which of the following is true ...and why? $$i) \ \ p_3 \cdot p_4 = p_4 \cdot p_3 \hspace{0.6in}vs.\hspace{0.6in} ii) \ \ p_3 \cdot p_5 = p_5 \cdot p_3$$
Express the permutation $(1,4,3,2)$ as a product/composition of only transpositions.
We see $p_1$ sends the element in position $1$ to position $5$, and $p_2$ then sends the element in position $5$ to position $1$. So collectively their combination (i.e., composition) sends the element in position $1$ to itself. As such we place a $1$ under the top $1$ in our composition. Similarly, $p_1$ sends the element in the $2^{nd}$ position to the $7^{th}$ position, and $p_2$ then sends the element in the $7^{th}$ position to the $5^{th}$ position. Thus we place a $5$ under the $2$ in the composition. Continuing in this way, we end up with the following permutation (using the bracket notation):
$\displaystyle{ \left[ \begin{array}{cccccccc} 1 & 2 & 3 & 4 & 5 & 6 & 7\\ 1 & 5 & 6 & 2 & 7 & 4 & 3 \end{array} \right] }$
Note in $p_1$, the element in position $1$ moves to position $5$, which in turn goes to $4$, before finally repeating things by going back to $1$. Thus, our first cycle is $(1,5,4)$. However, there are still positions unaccounted for that are moving. Position $2$ is among them, with this position going to position $7$, which then goes to position $3$, and then $6$, before returning to $2$. As such our second cycle is $(2,7,3,6)$. With no other positions (or positions changing), we arrive at the cycle notation for $p_1$:
$(1,5,4)(2,7,3,6)$
Let's build this product up one operation at a time: $\displaystyle{\begin{array}{rcl} p_3^2 \cdot p_4 \cdot p_5^{-1} &=& (1,2,6,4,7)^2 \cdot (3,5) \cdot \left[(1,3,4,7)(2,6)\right]^{-1}\\ &=& (1,6,7,2,4) \cdot (3,5) \cdot \left[(1,3,4,7)(2,6)\right]^{-1}\\ &=& (1,6,7,2,4) \cdot (3,5) \cdot (1,3,4,7)^{-1} (2,6)^{-1}\\ &=& (1,6,7,2,4) \cdot (3,5) \cdot (1,7,4,3) (2,6)\\ &=& (1,2,3,5)(4,7,6) \end{array}}$
Only (i) is true. Note $p_3$ and $p_4$ commute with each other as they are disjoint cycles. As for $p_3$ and $p_5$, note $p_3 \cdot p_5$ can be written as $(1,6,\cdots)$ while $p_5 \cdot p_3$ can be written as $(1,3,\cdots)$. These are definitely not equal.
Associativity
One way to accomplish this is by considering a braid (on $4$ strands) that permutes its strands in the same way. One example is $x_1 x_2 x_3$. Each crossing can be thought of as a transposition (a "swapping") of two strands. The first swaps strands $1$ and $2$, the second swaps $2$ and $3$, and the third swaps $3$ and $4$. This gives us the permutation as a product of transpositions:
$(1,4,3,2) = (1,2)(2,3)(3,4)$
Assume all variables are positive real values. Simplify each expression completely. In particular, write each without negative exponents; with no $n^{th}$ powers as a factor inside and $n^{th}$ root; and with no radicals or fractional exponents in denominators.
$\displaystyle{\frac{(3 a^2 b^{-3})^2}{(-2 a^{-1} b^{-2} c^{3})^3}}$
$\displaystyle{\frac{2}{\sqrt[3]{9x y^2}}}$ (write using radical notation)
$\displaystyle{\left[ \frac{27 x^{-1} y^3}{4 x^{-3} y^{-1} z} \right]^{-\frac{1}{2}}}$
$\displaystyle{\left( x^{\frac{2}{3}} y^{-\frac{1}{5}} x^{\frac{4}{5}} y^0 \right)^2}$
$\displaystyle{\sqrt{x^5 \sqrt[3]{y^2 \sqrt[5]{z^7}}}}$ (write using a single radical)
$\displaystyle{ \begin{array}[t]{rcl} \cfrac{(3 a^2 b^{-3})^2}{(-2 a^{-1} b^{-2} c^{3})^3} &=& \cfrac{9a^4 b^{-6}}{-8 a^{-3} b^{-6} c^9}\\ &=& \cfrac{9a^7}{-8c^9} \end{array}}$
$\displaystyle{ \begin{array}[t]{rcl} \cfrac{2}{\sqrt[3]{9x y^2}} &=& \cfrac{2}{(3^2 x y^2)^{1/3}}\\ &=& \cfrac{2}{3^{2/3} x^{1/3} y^{2/3}}\\ &=& \cfrac{2}{3^{2/3} x^{1/3} y^{2/3}} \cdot \cfrac{3^{1/3} x^{2/3} y^{1/3}}{3^{1/3} x^{2/3} y^{1/3}}\\ &=& \cfrac{2 \cdot 3^{1/3} x^{2/3} y^{1/3}}{3xy}\\ &=& \cfrac{2 \sqrt[3]{3x^2 y}}{3xy} \end{array}}$
$\displaystyle{ \begin{array}[t]{rcl} \displaystyle{\left[ \frac{27 x^{-1} y^3}{4 x^{-3} y^{-1} z} \right]^{-\frac{1}{2}}} &=& \displaystyle{\left[\cfrac{27x^2 y^4}{4z} \right]^{-\frac{1}{2}}}\\ &=& \displaystyle{\left[\cfrac{4z}{27x^2 y^4} \right]^{\frac{1}{2}}}\\ &=& \cfrac{2z^{1/2}}{3^{3/2} x y^2}\\ &=& \cfrac{2z^{1/2}}{3^{3/2} x y^2} \cdot \cfrac{3^{1/2}}{3^{1/2}}\\ &=& \cfrac{2z^{1/2} \cdot 3^{1/2}}{3^2 x y^2}\\ &=& \cfrac{2 \sqrt{3z}}{9xy^2} \end{array}}$
$\displaystyle{ \begin{array}[t]{rcl} \left( x^{\frac{2}{3}} y^{-\frac{1}{5}} x^{\frac{4}{5}} y^0 \right)^2 &=& \left( x^{\left(\frac{2}{3} + \frac{4}{5}\right)} y^{-\frac{1}{5}} \right)^2\\ &=& \left( x^{\frac{22}{15}} y^{-\frac{1}{5}} \right)^2\\ &=& x^{\frac{44}{15}} y^{-\frac{2}{5}}\\ &=& \cfrac{x^{\frac{44}{15}}}{y^{\frac{2}{5}}}\\ &=& \cfrac{x^{\frac{44}{15}}}{y^{\frac{2}{5}}} \cdot \cfrac{y^{\frac{3}{5}}}{{y^{\frac{3}{5}}}}\\ &=& \displaystyle{\frac{x^{\frac{44}{15}} y^{\frac{3}{5}}}{y}}\\ &=& \displaystyle{\frac{x^2 x^{\frac{14}{15}} y^{\frac{3}{5}}}{y}}\\ &=& \displaystyle{\frac{x^2 x^{\frac{14}{15}} y^{\frac{9}{15}}}{y}} \quad \textrm{or in radical notation,}\\ &=& \displaystyle{\frac{x^2 \sqrt[15]{x^{14} y^9}}{y}} \end{array}}$
$\displaystyle{\begin{array}[t]{rcl} \sqrt{x^5 \sqrt[3]{y^2 \sqrt[5]{z^7}}} &=& (x^5 (y^2 (z^7)^{1/5})^{1/3})^{1/2}\\ &=& (x^5 (y^2 z^{7/5})^{1/3})^{1/2}\\\\ &=& (x^5 y^{2/3} z^{7/15})^{1/2}\\\\ &=& x^{5/2} y^{2/6} z^{7/30}\\\\ &=& x^{2}x^{1/2} y^{2/6} z^{7/30}\\\\ &=& x^2 x^{15/30} y^{10/30} z^{7/30}\\\\ &=& x^2 \sqrt[30]{x^{15} y^{10} z^7} \end{array}}$
If an initial guess of $4$ is used to approximate $\sqrt{15}$, what is the next (and better) approximation for this square root if using the Babylonian method discussed in class? (You may leave your answer as a fraction, if desired.)
$\displaystyle{\frac{4 + \frac{15}{4}}{2} = \frac{\frac{16 + 15}{4}}{2} = \frac{31}{8}}$
Answer the questions below, concerning "triangle-of-power" notation:
Write the expression $\displaystyle{(\log_2 3 + \sqrt{3} + 2^3)}$ using triangle notation. (i.e., just translate each term to triangle notation -- you need not do anything further to the expression.)$\newcommand{\dotriangle}[1]{\raise{-0.7ex}{\vcenter{#1 \kern .2ex\hbox{$\triangle$}\kern.2ex}}}$ $\newcommand{\dtp}[3]{\vphantom{\dotriangle\LARGE}\Rule{-0.1em}{0pt}{2.5ex}_{\scriptstyle #1} {\overset{\scriptstyle #2} {\dotriangle\LARGE}}\Rule{0em}{0pt}{2.5ex}_{\scriptstyle #3}\Rule{0.1em}{0pt}{0ex}}$ $\newcommand{\itp}[3]{\vphantom{\dotriangle\normalsize}\Rule{-0.7ex}{0pt}{1.8ex}_{#1} \overset{#2}{\dotriangle\normalsize}\Rule{0pt}{0pt}{1.8ex}_{#3}\Rule{0ex}{-0.2em}{0pt}}$ $\newcommand{\stp}[3]{\vphantom{\dotriangle\normalsize}\Rule{-0.7ex}{0pt}{1.8ex}_{\scriptstyle #1} {\overset{\scriptstyle #2}{\dotriangle\normalsize}}\Rule{0pt}{0pt}{1.8ex}_{\scriptstyle #3}\Rule{0ex}{-0.2em}{0pt}}$ $\newcommand{\sstp}[3]{\vphantom{\dotriangle\normalsize}\Rule{-0.7ex}{0pt}{1.8ex}_{\scriptstyle #1} {\overset{\scriptstyle #2}{\dotriangle\normalsize}}\Rule{0pt}{0pt}{1.8ex}_{\scriptstyle #3}\Rule{0ex}{-0.2em}{0pt}}$ $\newcommand{\tripow}[3]{\mathop{\mathchoice{\dtp{#1}{#2}{#3}}{\itp{#1}{#2}{#3}}{\stp{#1}{#2}{#3}}{\sstp{#1}{#2}{#3}}}}$ $\newcommand{\vtp}[3]{\vcenter{\tripow{#1}{#2}{#3}}}$
Write the relationship $\vtp{x}{3}{5}$ three ways -- one using exponents, one using roots, and one using logarithms.
$\displaystyle{\vtp{2}{}{3} + \vtp{\vphantom{3}}{2}{3} + \vtp{2}{3}{}}$
$\displaystyle{x^3 = 5 \quad \quad x = \sqrt[3]{5} \quad \quad \log_x 5 = 3}$
Write an equivalent expression using no more than a single logarithm (you may assume $x,y \gt 0$):
$2\log_5 x - 3\log_5 2 + \frac{1}{3}\log_5 y^6$
$\displaystyle{\frac{(\log_x x^2)(\log_x 10)}{\log_x 2}}$
$\log_9 \sqrt{27} + 2^{\log_2 x} + \log_5 x$
$\displaystyle{ \begin{array}[t]{rcl} 2\log_5 x - 3\log_5 2 + \frac{1}{3}\log_5 y^6 &=& \log_5 x^2 - \log_5 2^3 + \log_5 y^2\\ &=& \log_5 \cfrac{x^2}{2^3} + \log_5 y^2\\ &=& \log_5 \cfrac{x^2 y^2}{8} \end{array}}$
$\displaystyle{ \begin{array}[t]{rcl} \displaystyle{\frac{(\log_x x^2)(\log_x 10)}{\log_x 2}} &=& \displaystyle{2 \cdot \frac{\log_x 10}{\log_x 2}}\\ &=& 2 \log_2 10 \end{array}}$
Just looking at the first term $\log_9 \sqrt{27}$ and given that $3$ provides a common base with which we can express both $9$ and $\sqrt{27}$, we hope to find the exponent needed on $9$ to get $\sqrt{27}$.
First, note $9^{1/2} = 3$. Then, "build up" from there to $\sqrt{27}$ by noting $(9^{1/2})^3 = 27$ and then noting $((9^{1/2})^3)^{1/2} = \sqrt{27}$. Finally, recalling $(a^b)^c = a^{(bc)}$ we multiply the exponents seen above to get $9^{3/4} = \sqrt{27}$. Thus, $\log_9 \sqrt{27} = \frac{3}{4}$.
Now we look at the second term and note $2^{\log_2 x} = x$ using one of our inverse properties involving logs.
Replacing the first two terms given the above calculations, we get as our answer: $$\displaystyle{\frac{3}{4} + x + \log_5 x}$$