|  |
With new functions introduced, we will want to know what their graphs look like and which (if any) are invertible. This will inevitably lead to questions about their domain and image/range as well. With all these ideas in mind, let us address the six trignometric functions discussed so far in their natural pairs:
First, as we can rotate a point $(x,y)$ about the origin on the unit circle as much or as little as we desire -- and in either a positive direction (i.e., counter-clockwise) or negative direction (clockwise) -- the coordinates $x = \cos \theta$ and $y=\sin \theta$ will always be defined. Hence, the domain of both the sine and cosine functions will be the set of all reals, $\mathbb{R}$.
As for the image/range, notice that the aforementioned point $(x,y)$ is contrained to fall on the unit circle. As such, neither coordinate may get larger than $1$ in magnitude. This combined with the fact that any horizontal line drawn whose distance from the $x$-axis does not exceed $1$ intersects the unit circle at least once (much more often twice), we can see the image/range of both sine and cosine will be the interval $[-1,1]$.
Recalling that multiple rotations around the unit circle can land one in the same position multiple times throughout that rotation. As such, the $x$ and $y$ coordinates -- and thus, the outputs of the $\cos \theta$ and $\sin \theta$ functions -- will be repeated whenever the related angles are co-terminal. Seeing the same ouputs for different input angles $\theta$ means the sine and cosine functions will not be invertible.
More generally, the lack of an inverse is a property shared by every periodic function. Recall we earlier defined periodic functions to be those functions with some non-zero value $p$ (which is called the function's period), where $f(x) = f(x+p)$ all $x$ in its domain. We also previously noted that the sine and cosine are clearly periodic (with period $p=2\pi$). Going further, note how the other four trigonometric functions are defined in terms of these two periodic functions, sine and cosine. As such, all six trigonometric functions must be periodic, and hence none will be invertible!
Still, as we have done in the past to other non-invertible functions, we can often restrict their domain to produce a related function that is invertible. For example, $f(x) = x^2$ becomes invertible if we restrict its domain to all real $x$ where $x \ge 0$. We try of course, when we restrict the domain, to ensure that every output attained by the original (non-invertible) function is also attained by the function with the restricted domain. There are often many ways to do this -- especially for periodic functions. The below shows the standard way this is accomplished for the sine function.
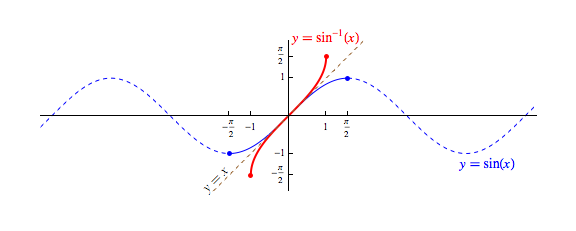
Note, the inputs above are given as radian measures, and we have switched to using an input variable of $x$ inside parentheses instead of a $\theta$ without parentheses so that we might draw both graphs on the same axes. Note that (traditionally) the use of $\theta$ as a variable suggests its value should be interpreted as an angle. Contrast this with the fact that the input to $sin^{-1}(x)$ is always a $y$-coordinate -- definitely not an angle! As such, we really should avoid using $\theta$ as an input variable for $sin^{-1}$. However, the use of the variable $x$ (and $y$ and $z$) traditionally only suggests the associated value(s) are real numbers -- which both the measure of an angle in radians and the value of a sine certainly would both be!
Note that for the purpose of creating a related inverse function, we have chosen to restrict the domain to $[\frac{\pi}{2},\frac{\pi}{2}]$. This is useful on a couple of fronts. Not only do we produce an invertible function (shown in solid blue), but we also produce one that has the exact same range as the sine function with an unrestricted domain.
Additionally, while there are several intervals that do both of these things (e.g., $[\pi/2,3\pi/2]$, $[-3\pi/2,-5\pi/2]$, etc.), the interval $[-\pi/2,\pi/2]$ minimizes the magnitudes of the angles involved.
We call the inverse to the restricted-domain version of the sine function (drawn above in red) the arcsine function, denoting it by either by $\arcsin x$, or $\sin^{-1} x$. The first name probably stems from the fact that it gives as output the measure of an "arc" (or angle) that has a given sine value.
This function behaves in many ways (but not all) as an inverse to the unrestricted domain version of $\sin x$.
For instance,
Like most inverse function pairs, the domain of $\sin^{-1} x$ is identical to the range of the $\sin x$, both being $[-1,1]$. However, the range of $\sin^{-1} x$ is only $[\pi/2,\pi/2]$, a small subset of the domain of the $\sin x$.
For any $x$ in the domain of $\sin^{-1}$, we have $\sin(\sin^{-1} x) = x$. However, $\sin^{-1} (\sin x) = x$ is true only if $x \in [-\pi/2,\pi/2]$ and false otherwise!
As always, notice the symmetry across the line $y=x$ between a function and its inverse (here, the un-named solid blue function with a restricted domain and the solid red arcsine function).
In a similar way, we can create a new invertible function that is identical to the cosine function, except with a restricted domain of $[0,\pi]$, to create a "pseudo-inverse" to the cosine function we call the arccosine function. The choice of the restricted domain here keeps the inputs as small as possible (and positive), which means the outputs of the related inverse function, called the arccosine function will also be as small as possible and positive. We denote the arccosine function by either $\arccos(x)$ or $\cos^{-1}(x)$:

Addressing first the domain of these two functions, recall again that $$\tan \theta = \frac{\sin \theta}{\cos \theta} \quad \textrm{ and } \quad \csc \theta = \frac{\cos \theta}{\sin \theta}$$ The quotients seen above open the door to some possible domain issues, should the denominators be zero. Indeed, noting that $\cos = 0$ (i.e., one touches the $y$-axis) with every half-circle rotation from $\frac{pi}{2}$ (i.e., $90^{\circ}$), we must exclude all $\theta = \frac{\pi}{2} + n\pi$ where $n$ is an integer, from the domain of the tangent function. That is to say, the domain of the tangent is $$\{x \in \mathbb{R} \ | \ x \neq \frac{\pi}{2} + n\pi, \, \textrm{ whenever } \, n \in \mathbb{Z}\}$$ Similarly, since $\sin \theta = 0$ (i.e., one touches the $x$-axis) with every half-circle rotation from $0$, we will need to exclude all integer multiples of $\pi$ from the domain of the cotangent function. Equivalently, the domain of the cotangent function is given by $$\{x \in \mathbb{R} \ | \ x \neq n\pi, \, \textrm{ whenever } \, n \in \mathbb{Z}\}$$
Regarding the image/range for each of these functions, recall the image shared earlier showing the magnitudes of these functions as segment lengths:
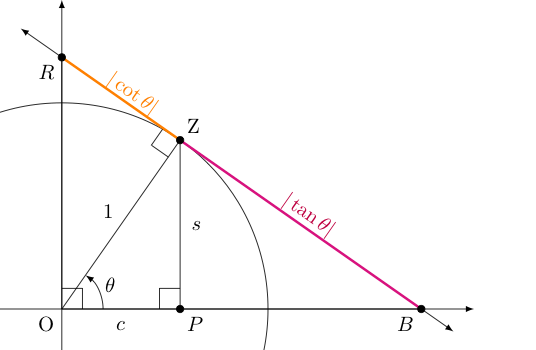
By letting $\theta$ approach $\pi/2$ (i.e., $90^{\circ}$) the purple segment with length equal to the magnitude of the tangent function grows without bound. If $\theta$ instead approaches $0$ this purple length can surely be made as small as desired (including zero). Had we constructed a similar image in the second quadrant, where $\tan \theta = \frac{\sin \theta}{\cos \theta}$ is negative, we would see a similar span of magnitudes possible. Combining these, the value of $\tan(x)$ ranges over all (positive or negative) real values, $\mathbb{R}$. Finding the range of the cotangent function works similarly, and is again all reals, $\mathbb{R}$.
As we see the magnitude of $\tan(x)$ growing without bound (either in a positive or negative way) as $x$ approaches each odd multiple of $\frac{\pi}{2}$, we can expect to see some vertical asymptotes in its graph. In the image below, we can see these asymptotes drawn as vertical, dashed blue lines (they are not part of the function!)
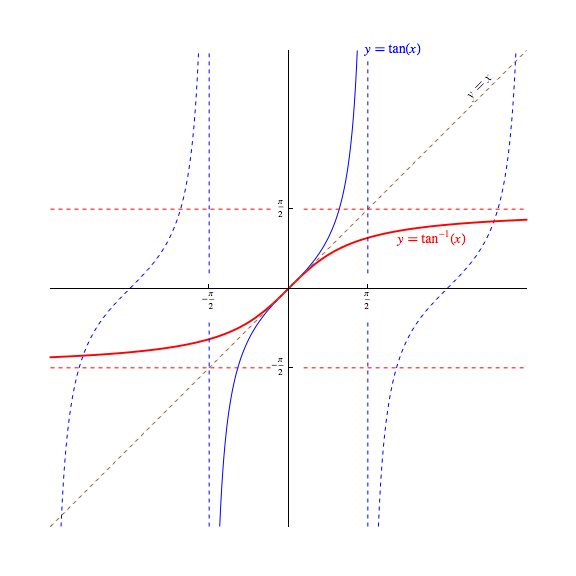
Switching discussion to the graphs and invertibility of these two functions, note that -- as mentioned before -- their periodic nature prohibits them from having inverses. However, we are free to construct for each a related domain-restricted function with an identical image/range that is invertible.
Traditionally, we restrict the domain of the tangent function to $(-\frac{\pi}{2},\frac{\pi}{2}$) so that graph can be drawn as a single continuous curve. Note in particular that the endpoints at $\pm\frac{\pi}{2}$ are not included in the restricted domain here, unlike the corresponding function used to produce $\arcsin(x)$. We call the inverse to this restricted-domain version of $\tan(x)$ the arctangent function, denoting it by $\arctan(x)$ or $\tan^{-1}(x)$.
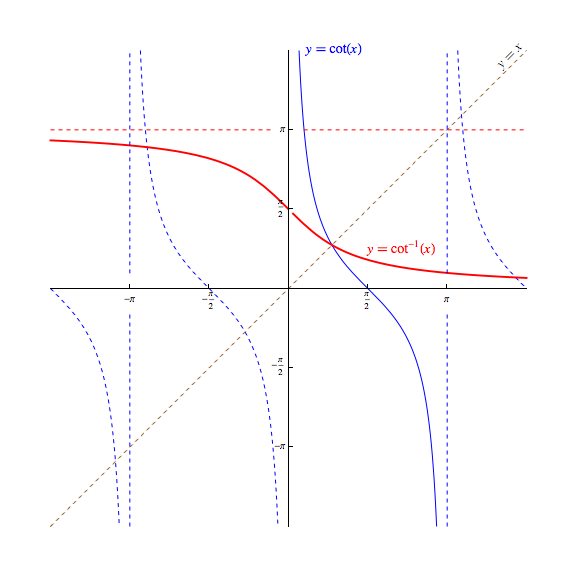
Interestingly, the choice for which "piece" of the cotangent function to invert to produce the arccotangent function is not universally agreed upon. We choose to define it to be $(0,π)$ so that the resulting arccotangent function, denoted $\textrm{arccot}(x)$ or $\cot^{-1}(x)$, is continuous and defined everywhere, and behaves in a manner more consistent with that seen in the related $\tan^{−1}(x)$ function.
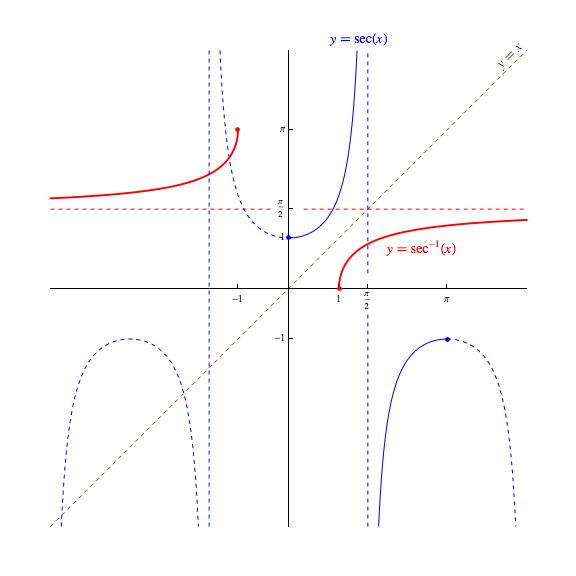
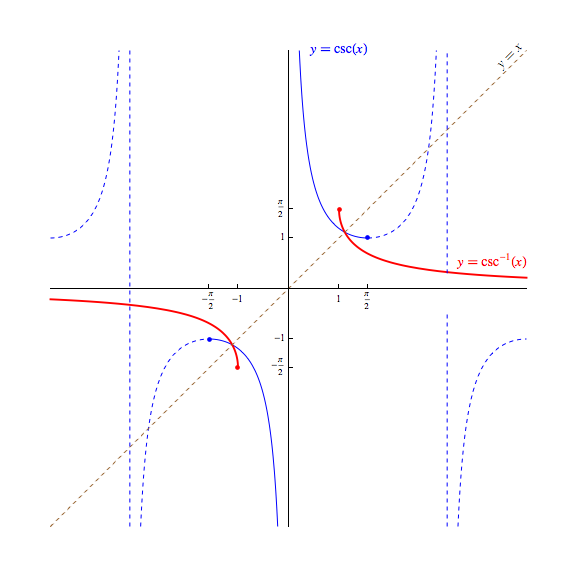
Finally, let us consider $\sec(x)$ and $\csc(x)$.
With regard to their domains, we can see in formulas describing these functions in terms of sine and cosine, we again have domain issues to worry about. $$\sec \theta = \frac{1}{\cos \theta} \quad \textrm{ and } \quad \csc \theta = \frac{1}{\sin \theta}$$ The denominators force these functions to have the same domains as the tangent and cotangent functions, respectively, with the domain of the secant function being $$\{x \in \mathbb{R} \ | \ x \neq \frac{\pi}{2} + n\pi, \, \textrm{ whenever } \, n \in \mathbb{Z}\}$$ and the domain of the cosecant function being $$\{x \in \mathbb{R} \ | \ x \neq n\pi, \textrm{ whenever } \, n \in \mathbb{Z}\}$$ Since both functions are reciprocals of a function with image/range $[-1,1]$ (all real values whose magnitude is on or less than $1$) the $\sec(x)$ and $\csc(x)$ functions must have a range of all real values whose magnitude exceed $1$! That is to say, the range of both secant and cosecant is $$\{x \in \mathbb{R} \ | \ |x| \ge 1\} = (-\infty,-1] \cup [1,\infty)$$
As another shared trait with the tangent and cotangent functions, note that being reciprocals of the cosine and sine function, as either $\cos(x)$ or $\sin(x)$ gets closer and closer to zero, the magnitude of either the $sec(x)$ or $\sin(x)$ respectively, again grows without bound. Thus, we can again expect vertical asymptotes in the graphs of the secant and cosecant funtions. Below, the blue dashed vertical lines represent these asymptotes -- these vertical lines should once again not be considered as points on the function!.
With regard to the graph of their associated "arc" functions, there is also (sadly) no universal agreement how to restrict the domain of each to create an invertible function. We choose here to define the arcsecant and arccosecant functions by choosing domain restrictions of $[0,\frac{\pi}{2}) \cup (\frac{\pi}{2},\pi]$ and $[-\frac{\pi}{2},0) \cup (0,\frac{\pi}{2}]$, denoting the "arc" functions thus created in the typical ways: