• About
• Statistics
• Number Theory
• Java
• Data Structures
• Cornerstones
• Calculus

Trigonometric Identities and More Complex Connections

An identity is an equation whose left and right sides are equal for all values of the variables in their respective implicit domains. Some trigonometric identities (i.e., identities involving trigonometric functions) that prove useful in a great many contexts are given below, with a discussion of why each must hold. While all of these identities can be proven without appealing to complex numbers, some are proven far more easily with them!

• The Pythagorean Identities:

  $$\begin{array}{c} \cos^2 \theta + \sin^2 \theta = 1\\ 1 + \tan^2 \theta = \sec^2 \theta\\ 1 + \cot^2 \theta = \csc^2 \theta \end{array}$$

  We have already discussed the first in the list above -- which is an immediate result of how we measure the magnitude of $|z|$ for some $z = \cos(\theta) + i \sin(\theta)$ on the unit circle (i.e., when $|z| = 1$). Recall, $|z|^2 = Re(z)^2 + Im(z)^2$

  The other two pythagorean identities listed are quick consequences of this relationship. The first being the result of dividing both sides by $\cos^2 \theta$, and the second being the result of dividing both sides by $\sin^2 \theta$ instead, as the calculations below reveal:

  $$\begin{array}{c|c} \displaystyle{\frac{\cos^2 \theta}{\cos^2 \theta} + \frac{\sin^2 \theta}{\cos^2 \theta} = \frac{1}{\cos^2 \theta}} \quad & \quad \displaystyle{\frac{\cos^2 \theta}{\sin^2 \theta} + \frac{\sin^2 \theta}{\sin^2 \theta} = \frac{1}{\sin^2 \theta}}\\\\ 1 + \tan^2 \theta = \sec^2 \theta & 1 + \cot^2 \theta = \csc^2 \theta \end{array}$$

• The Even/Odd Identities

  $$\begin{array}{rcl} \cos (-\theta) &=& \phantom{-}\cos \theta\\ \sin (-\theta) &=& -\sin \theta\\ \tan (-\theta) &=& -\tan \theta \\ \end{array}$$

  Examining the next picture immediately reveals the three "even/odd function identities" given above. (You do of course remember how we defined "even" and "odd" functions when we introduced functions of the form $(x) = x^n$, right?) To see how these three results can be deduced, consider the image below. Note the right triangles, sharing a common acute angle and hypotenuse length, must consequently be congruent. As such, the vertical sides of each are the same length.

  

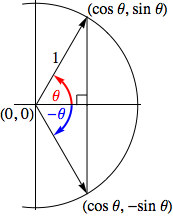
  The common length of the vertical sides tell us the associated $y$-coordinates for the red and blue angles have opposite signs, but the same magnitude, which in turn implies $\sin (-\theta) = -\sin \theta$.

  Meanwhile, the horizontal side common to both triangles tells us the associated $x$-coordinates for these angles are identical, and thus $\cos (-\theta) = \cos \theta$.

  Knowing the values of the sine and cosine for $-\theta$, we can find the tangent for this angle as well,

  $$\tan (-\theta) = \frac{\sin (-\theta)}{\cos (-\theta)} = \frac{-\sin \theta}{\cos \theta} = -\tan \theta$$

• The Complementary Angle Identities

  $$\begin{array}{rcl|rcl} \sin(\pi/2 - \theta) &=& \cos \theta & \cos(\pi/2 - \theta) &=& \sin \theta\\ \sec(\pi/2 - \theta) &=& \csc \theta & \csc(\pi/2 - \theta) &=& \sec \theta\\ \tan(\pi/2 - \theta) &=& \cot \theta & \cot(\pi/2 - \theta) &=& \tan \theta\\ \end{array}$$

  Why these hold has already been discussed. They are included here only as we should now start thinking of these as tools to argue more interesting results.

• The Sum and Difference Identities

  $$\begin{array}{c} \cos(\alpha \pm \beta) = \cos \alpha \cos \beta \mp \sin \alpha \sin \beta\\ \sin(\alpha \pm \beta) = \sin \alpha \cos \beta \pm \cos \alpha \sin \beta\\\\ \tan(\alpha \pm \beta) = \displaystyle{\frac{\tan \alpha \pm \tan \beta}{1 \mp \tan \alpha \tan \beta}}\\ \end{array}$$

  Proofs of these three identities particularly benefit from defining trig functions in terms of complex numbers! Consider the below:

  $$\begin{array}{rcl} \textrm{cis}(\alpha \pm \beta) &=& \textrm{cis}(\alpha) \cdot \textrm{cis}(\pm \beta)\\ &=& (\cos \alpha + i \sin \alpha )(\cos \beta + i \sin(\pm \beta))\\ &=& (\cos \alpha + i \sin \alpha )(\cos \beta \pm i \sin \beta ) \quad {\scriptstyle {\textrm{taking advantage of the even/odd property for $\sin(x)$}}}\\ &=& \left[\cos \alpha \cos\beta \mp \sin \alpha \sin \beta \right] + \left[\sin \alpha \cos \beta \pm \cos \alpha \sin \beta \right] \cdot i \end{array}$$ Note the last line above results from simply expanding the product immediately before, replacing $i^2$ with $-1$, and collecting the remaining multiples of $i$ together.

  Now recall that $z_{\alpha \pm \beta}$ is on the unit circle, so its real part and imaginary coefficient give the cosine and sine values of its argument, $\alpha \pm \beta$, respectively. Thus, the first and second sum and difference identities are immediately established! $\require{cancel}$

  All that remains is to prove the related result for the tangent. Fortunately, once the above identities are established, this one is trivial:

  $$\begin{array}{rcll} \tan (\alpha \pm \beta) &=& \displaystyle{\frac{\sin \alpha \cos \beta \pm \cos \alpha \sin \beta}{\cos \alpha \cos \beta \mp \sin \alpha \sin \beta}}\\\\ &=& \frac {\displaystyle{\frac{\sin \alpha \cancel{\cos \beta}}{\cos \alpha \cancel{\cos \beta}} \pm \frac{\cancel{\cos \alpha} \sin \beta}{\cancel{\cos \alpha} \cos \beta}}} {\displaystyle{\frac{\cancel{\cos \alpha \cos \beta}}{\cancel{\cos \alpha \cos \beta}} \mp \frac{\sin \alpha \sin \beta}{\cos \alpha \cos \beta}}} & \overset{\normalsize{\textrm{after dividing by } \cos \alpha \cos \beta}}{\scriptsize{\textrm{to introduce tangents}}}\\\\ &=& \displaystyle{\frac{\tan \alpha \pm \tan \beta}{1 \mp \tan \alpha \tan \beta}} \end{array}$$

• The Double and Triple Angle Identities

  $$\begin{array}{c} \cos 2\theta &=& \cos^2 \theta - \sin^2 \theta\\ \sin 2 \theta &=& 2 \sin \theta \cos \theta\\\\ \cos 3\theta &=& \cos^3 \theta - 3\cos \theta \sin^2 \theta\\ \sin 3\theta &=& 3\cos^2 \theta \sin \theta - \sin^3 \theta \end{array}$$

  Directly applying the sum formula to $\cos (\theta + \theta)$ and $\sin (\theta + \theta)$ would quickly give us formulas for $\cos 2\theta$ and $\sin 2\theta$, but we instead again appeal to complex numbers as doing so provides an efficient way to establish more general results.

  To see this, consider the below -- noting how the special product rules for the squares and cubes of binomials play a significant role. As a reminder of these special product rules, recall that $(a+b)^2 = a^2 + 2ab + b^2$ and $(a+b)^3 = a^3 + 3a^2b + 3ab^2 + b^3$.

  Similar to how we began to prove the sum and difference formulas, $$\begin{array}{rcl} \textrm{cis}(2\theta) &=& \textrm{cis}^2(\theta)\\ &=& (\cos \theta + i \sin \theta)^2\\ &=& \cos^2 \theta + 2i\sin \theta \cos \theta + i^2 \sin^2 \theta \quad {\scriptstyle {\textrm{by the special product rule for $(a+b)^2$}}}\\ &=& (\cos^2 \theta - \sin^2 \theta) + (2\sin \theta \cos \theta) \cdot i \quad {\scriptstyle {\textrm{recalling that $i^2 = -1$ and then collecting terms}}} \end{array}$$ As argued before for the sum and difference formulas, remember that $z_{2\theta}$ is on the unit circle, so its real part and imaginary coefficient give the values of $\cos 2\theta$ and $\sin 2\theta$ seen in the box above.

  To find the triple angle formula we proceed similarly, noting: $$\begin{array}{rcl} \textrm{cis}(3\theta) &=& \textrm{cis}^3(\theta)\\ &=& (\cos \theta + i \sin \theta)^3\\ &=& \cos^3 \theta + 3(\cos^2 \theta)(i\sin \theta) + 3(\cos \theta)(i^2 \sin^2 \theta) + i^3 \sin^3 \theta \, \, {\scriptstyle {\textrm{by the special product rule for $(a+b)^3$}}}\\ &=& (\cos^3 \theta - 3\cos \theta \sin^2 \theta) + (3\cos^2 \theta \sin \theta - \sin^3 \theta) \cdot i \quad {\scriptstyle {\textrm{recalling that $i^2 = -1$, and therefore $i^3 = -i$}}} \end{array}$$ Again recalling $z_{3\theta}$ is on the unit circle, its real part and imaginary coefficient must give the values for $\cos 3\theta$ and $\sin 3\theta$ also seen in the box above.

• Alternate Forms for the Double Angle Identities

  $$\begin{array}{rcl|rcl} \cos 2\theta &=& 2\cos^2 \theta - 1 \phantom{abc} & \phantom{abc} \cos 3\theta &=& 4\cos^3 \theta - 3\cos \theta\\ &=& 1 - 2\sin^2 \theta & \sin 3\theta &=& 3\sin \theta - 4\sin^3 \theta\\ \end{array}$$

  The Pythagorean identity $\cos^2 \theta + \sin^2 \theta = 1$ provides an easy way to find an alternate form for any expression involving either $\cos^2 \theta$ or $\sin^2 \theta$, as we may solve it for these two expressions to find $$\cos^2 \theta = 1 - \sin^2 \theta \quad \textrm{ and } \quad \sin^2 \theta = 1 - \cos^2 \theta$$ Note that when we apply these to the double-angle identity for cosine, we can produce replacements for $\cos 2\theta$ that involve only a single trigonometric function. To see this, consider the following. $$\begin{array}{rcl} \cos 2\theta &=& \cos^2 \theta - \sin^2 \theta\\ &=& \cos^2 \theta - (1 - \cos^2 \theta)\\ &=& 2\cos^2 \theta - 1 \end{array}$$

  and

  $$\begin{array}{rcl} \cos 2\theta &=& \cos^2 \theta - \sin^2 \theta\\ &=& (1 - \sin^2 \theta) - \sin^2 \theta\\ &=& 1 - 2 \sin^2 \theta \end{array}$$

  We may do something similar with the triple angle formulas, as seen below: $$\begin{array}{rcl} \cos 3\theta &=& \cos^3 \theta - 3\cos \theta \sin^2 \theta\\ &=& \cos^3 \theta - 3\cos \theta (1-\cos^2 \theta)\\ &=& \cos^3 \theta - 3\cos \theta + 3\cos^3 \theta\\ &=& 4\cos^3 \theta - 3\cos \theta \end{array}$$ and $$\begin{array}{rcl} \sin 3\theta &=& 3\cos^2 \theta \sin \theta - \sin^3 \theta\\ &=& 3(1-\sin^2 \theta) \sin \theta - \sin^3 \theta\\ &=& 3\sin \theta - 3\sin^3 \theta - \sin^3 \theta\\ &=& 3\sin \theta - 4\sin^3 \theta \end{array}$$

• The Half-Angle Identities

  Lastly, if we take these two alternate forms for $\cos 2\theta$ and solve for $\sin^2 \theta$ and $\cos^2 \theta$, respectively -- we produce the half angle identities,

  $$\begin{array}{rcl} \cos^2 \theta &=& \displaystyle{\frac{1+\cos 2\theta}{2}}\\\\ \sin^2 \theta &=& \displaystyle{\frac{1-\cos 2\theta}{2}}\\ \end{array}$$

  Knowing the half angle identities in the above form will be the most useful for applications in calculus. That said, why these identities are called the "half angle" identities is made more clear upon making a substitution of $x = 2\theta$ and then taking a square root:

  $$\begin{array}{c} \left| \cos \left( \frac{x}{2} \right) \right| &=& \displaystyle{\sqrt{\frac{1+\cos x}{2}}}\\\\ \left| \sin \left( \frac{x}{2} \right) \right| &=& \displaystyle{\sqrt{\frac{1-\cos x}{2}}} \end{array}$$

  In this way, we can discover the magnitudes of the sine and cosine for half an angle if we know the cosine of the full angle. As for whether the sine and cosine are positive or negative, this is most easily managed by determining in which quadrant the half angle lies.

Proving Other Trigonometric Identities

To prove that a trigonometric equation is an identity, one typically starts by trying to show that either one side of the proposed equality can be transformed into the other, or that both sides can be transformed into the same expression.

In other words, suppose $A$ and $B$ are some trigonometric expressions and we are trying to determine if $A=B$.

We hope that both expressions will simplify to some common form $C$, as if we can show the following:

then we will know

and thus,

That is our general "plan of attack" -- although, we might get lucky and the sequence of $A_1, A_2, \cdots$ will terminate in $B$, or the sequence $B_1, B_2, \cdots$ will terminate in $A$, which then shortens our argument a bit.

There are some basic strategies to help us get to that common form $C$ as efficiently as possible:

• Only manipulate one side of the proposed identity at a time. Start by attempting to simplify the more complicated side first, as which steps one should take will likely be more obvious for this side.

• First "trigonometrically simplify" the side in question.

  • One should try rewriting all of trigonometric functions involved in terms of sines and cosines, unless there is a compelling reason not to do this.

    Example

    $$\begin{array}{rcl} \tan \theta + 2\csc \theta &=& \displaystyle{\left( \frac{\sin \theta}{\cos \theta} \right) + 2\left( \frac{1}{\sin \theta} \right)}\\ &=& \cdots \end{array}$$

  • Likewise, if you see trigonometric functions involving more than one angle measure, try to use known identities to rewrite things so that only a single angle measure is involved.

    Example

    $$\begin{array}{rcl} \displaystyle{\frac{\cos 2\theta + \sin \theta}{\sin 2\theta + \sin(-\theta)}} &=& \displaystyle{\frac{ (\cos^2 \theta - \sin^2 \theta) + \sin \theta}{2\sin \theta \cos \theta - \sin \theta}}\\ &=& \cdots \end{array}$$

  • If one side can be written in terms involving (perhaps multiple occurrences of) a single trigonometric function of a single angle measure, doing so may help. In particular, this often helps in cases where one side of the proposed identity is already in this form, and the other side consists of a mixture of trigonometric functions.

    Example

    $$\begin{array}{rcll} \displaystyle{\frac{\cos 2\theta}{\cos(\pi/2-\theta)}} &=& \displaystyle{\frac{1 - 2\sin^2 \theta}{\sin \theta}} & \overset{\normalsize{\textrm{assuming we were trying to get}}}{\scriptsize{\textrm{things in terms of only sine functions}}}\\ &=& \cdots \end{array}$$

• As the previous examples attest, trigonometrically simplifying an expression sometimes makes it algebraically more cumbersome. This can actually be a good thing -- as it gives us a direction to proceed. Specifically -- after trigonometrically simplifying a side of the proposed identity -- one can next focus on "algebraically simplifying" it.

  • Complex fractions (i.e., fractions with fractions in either the numerator or denominator) should be collapsed

    Example

    $$\begin{array}{rcll} \frac{\displaystyle{\frac{\sin \theta}{\cos^2 \theta}}}{\displaystyle{1 + \frac{1}{\cos \theta}}} &=& \displaystyle{\frac{\sin \theta}{\cos^2 \theta + \cos \theta}} & \scriptsize{\textrm{ after multiplying by } \displaystyle{\frac{\cos^2 \theta}{\cos^2 \theta}}}\\ &=& \cdots \end{array}$$

  • When fractional expressions appear in a sum or difference, these terms should be combined into a single fraction, finding common denominators as necessary. The resulting fractional expression may, upon factoring, admit a common factor that can be cancelled -- or may be simplified in some other fashion.

    Example$\require{cancel}$

    $$\begin{array}{rcll} \displaystyle{\frac{1}{\sin^2 \theta} + \frac{1}{\cos^2 \theta} + \frac{\sin \theta \cos^2 \theta - 1}{\sin^2 \theta \cos^2 \theta}} &=& \displaystyle{\frac{\cos^2 \theta + \sin^2 \theta - 1 + \sin \theta \cos^2 \theta}{\sin^2 \theta \cos^2 \theta}}\\\\ &=& \displaystyle{\frac{1 -1 + \sin \theta \cos^2 \theta}{\sin^2 \theta \cos^2 \theta}}\\\\ &=& \displaystyle{\frac{\sin \theta \cos^2 \theta}{\sin^2 \theta \cos^2 \theta}}\\\\ &=& \displaystyle{\frac{1}{\sin \theta}}\\\\ &=& \cdots \end{array}$$

• Try to manipulate the side in question into the same "form" as the other side. For example, suppose one is attempting to simplify the left side of a proposed identity and the right side is a product. Then one should attempt to factor the left side, so that it is also expressed as a product.

  Also, when the left and right sides get to the point where there is a partial "match", one should leave the matched parts alone from that point forward, and only manipulate the parts that still don't look like one another.

  Example

  Show $\sin \theta \cos^2 \theta - \sin \theta = -\sin^3 \theta$ is an identity.

  Starting with the left side, we have...

  $$\begin{array}{rcll} \sin \theta \cos^2 \theta - \sin \theta &=& \sin \theta (\cos^2 \theta - 1) & \overset{\normalsize{\textrm{notice the right side, } -\sin^3 \theta, \textrm{ is a product, so}}}{\scriptsize{\textrm{we factor the left side to have the same form}}}\\\\ &=& \cdots\\\\ &=& \sin \theta (-\sin^2 \theta) & \overset{\normalsize{\textrm{working backwards from the sought expression below}}}{\scriptsize{\textrm{we expose a "match" of } \sin \theta \textrm{ with the above}}}\\\\ &=& -\sin^3 \theta\\\\ \end{array}$$

  To fill in the missing steps above, we just need to "massage" $(\cos^2 \theta - 1)$ into $(-\sin^2 \theta)$. This of course is immediate, given the Pythagorean identity $\cos^2 \theta + \sin^2 \theta = 1$.

Showing an Equation is Not an Identity

It may be the case that in the course of trying to prove a given equation is an identity, one begins to suspect that it is not.

In such situations, one should test whether the equation's left and right sides are actually equal by plugging in some values for the variables it contains. Remember, one only needs a single counter-example to prove an equation is not an identity.

If however, one tests a particular value (or set of values) and the left and right sides of the given equation agree in value, that particular test is inconclusive -- and a decision must be made whether to continue the search for a counter-example and test additional values, or to return to trying to prove the given equation is an identity.

To have the best chance of selecting values that will show a given equation is not an identity, one should keep the following in mind:

• While picking angle measures that are integer multiples of $\pi/2$ will lend itself to easy evaluation of the expressions involved in the equation, such values will often fail to reveal an equation is not an identity due to the fact that either the sine or cosine for these angle measures will be zero.

  Example

  The following is clearly not an identity:     $\sin \theta = \cos \theta + \sin \theta$. However, if one tests this with either $\theta = \pi/2$ or $\theta = 3\pi/2$, the results will be inconclusive, as the left and right sides will have the same value (i.e., $1$ in the first case, $-1$ in the second).

• A similar problem presents itself when testing a proposed identity with angle measures that are odd integer multiples of $\pi/4$, but for a different reason. For these angle measures, recall the sine and cosine values are either identical or differ only in sign. This too can create inconclusive results for an equation that is not actually an identity.

  Example

  The following is clearly not an identity:     $2\sin \theta= \cos \theta + \sin \theta$. However, if one tests this with either $\theta = \pi/4$ or $\theta = 5\pi/4$, the results will be inconclusive, as both sides evaluate to $\sqrt{2}$.

• Testing a proposed identity with angle measures that are integer multiples of $\pi/6$ or $\pi/3$ (when reduced) can be good first choices, as the exact values of the trigonometric functions are easy to find, and the problems seen above don't occur.