

 |  |
We have seen how one can approximate the area under a non-negative function and above the $x$-axis with a Riemann sum, with better approximations occuring when the norm of the related partition is very small (close to zero). In the limiting case when $\lVert\Delta x\rVert \rightarrow 0$, we produce the best approximation -- the exact area under the function in question! Recalling that a definite integral is the limit of a Riemann sum (when it exists), we can thus express such areas as definite integrals of the related functions.
To do this in practice, recall that when approximating such an area, we started by slicing it into very thin rectangles. The $i^{th}$ rectangle's width was the (presumabley small) difference of $x$-coordinates at the two ends of the $i^{th}$ sub-interval, $\Delta x_i$, and its height was given by evaluating the function at some $x$-coordinate, $x_i^*$ between these endpoints.
Summing these rectangular areas to approximate the overall area, and taking a limit as $\lVert\Delta x\rVert \rightarrow 0$, we produce a definite integral. Supposing the non-negative function in question was $f$, and that we sought the area under that function (and above the $x$-axis) between $x=a$ and $x=b$, the area could thus be expressed as $$\textrm{Area } = \int_a^b f(x)\,dx$$
Consider the following concrete example,
|
Example Find the area under $f(x) = -x^2+4x$ and above the $x$-axis between $x=0$ and $x=4$. Solution First, note that $f(x)$ is easily seen to be non-negative on $[0,4]$ upon drawing its graph. Now, imagine the area in question sliced up into thin vertical strips and the approximating rectangles for each of these strips. In the diagram below, one of these approximating rectangles is shown in magenta. 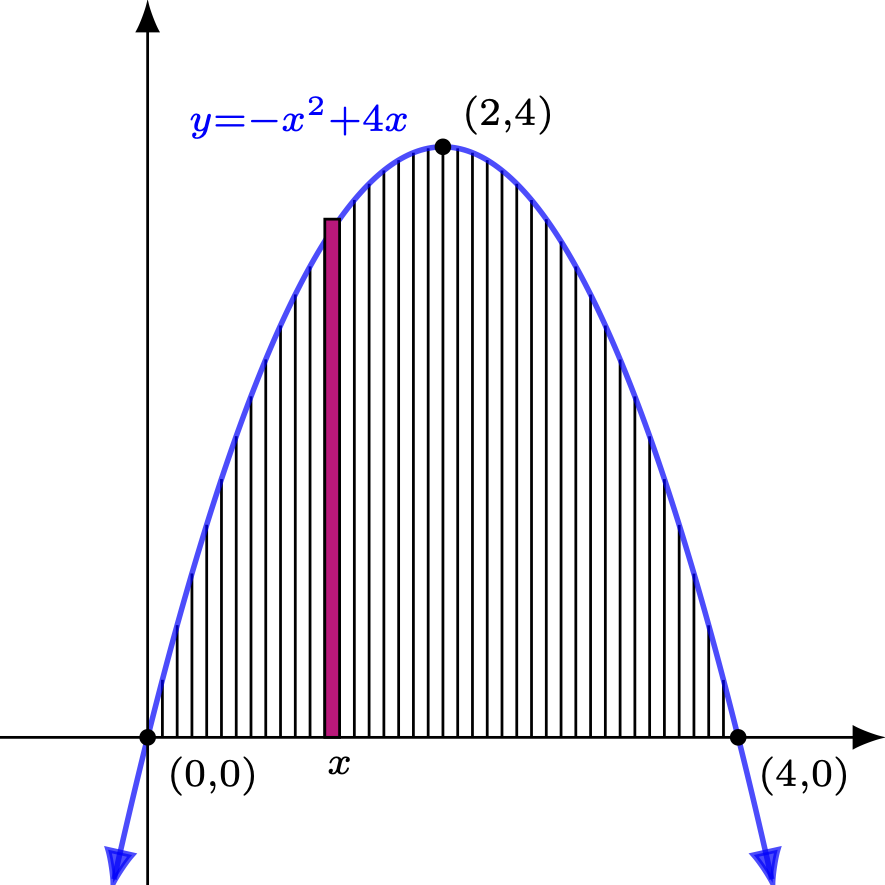 Note that the height of the rectangle is given by $f(x) = -x^2 + 4x$ for some $x$ (here, the right endpoint of the appropriate $i^{th}$ sub-interval). Assuming a regular partition, the width being a horizontal distance will then be given by some difference of $x$-coordinates, $\Delta x$. We could at this point build the Riemann sum (shown below) that would lead to the definite integral, if so desired. Just let the $x$ value for the $i^{th}$ rectangle be denoted by $x_i^*$, as we have done in the past: $$\sum_{i=1}^n \underbrace{[-(x_i^*)^2 + 4(x_i^*)]}_{\textrm{height}} \, \underbrace{\Delta x}_{\textrm{width}}$$ However, we can shortcut this process by realizing that the width of the rectangle, as we take a limit as $\lVert \Delta x \rVert \rightarrow 0$, effectively turns into the $dx$ in the corresponding definite integral. Also, in the limit the individual $x_i^*$ values don't matter as much as the fact that we are essentially considering all the $x$ values our sought area spans. With these thoughts in mind, note that the right side of the definite integral we seek can still be thought of as a product of a height and width for an (infinitesimally thin) rectangle: $$\underbrace{(-x^2 + 4x)}_{\textrm{height}}\,\underbrace{dx}_{\textrm{width}}$$ Noticing that the span of $x$ values that correspond to approximating rectangles with the height and width described above includes all those values between $x=0$ and $x=4$ completes the picture, as these two values provide us with the limits of integration on our definite integral. Putting everything together, we have the area under $f(x)$ and above the $x$-axis given by $$\int_0^4 (-x^2+4x)\,dx$$ We can now appeal to the fundamental theorem of calculus to evaluate this definite integral, as seen below $$\begin{array}{rcl} \displaystyle{\int_0^4 (-x^2+4x)\,dx} &=& \displaystyle{\left. \left( -\frac{1}{3}x^3 + 2x^2 \right) \right|_0^4}\\ &=& \displaystyle{-\frac{64}{3} + 32}\\ &=& \displaystyle{\frac{32}{3}} \end{array}$$ |
Importantly, we can find an area sought, like the one in the example above, in more than one way.
Consider if we had instead sliced the area in the example above into thin horizontal strips and considered the approximating rectangles for these instead.
Then, the dimension of the rectangle that "gets small" in the limit will no longer be the width, but rather its height. This height, being a vertical distance, is thus expressible as a difference of $y$-coordinates. Calling this distance $\Delta y$ suggests that if we can find the width in terms of $y$, we can setup a definite integral where $y$ is the variable of integration that also gives us the area sought. Equivalently, the area can be expressed by a definite integral with a $dy$ at the end, with the function integrated being a function of $y$, and with the limits of integration being $y$-values.
Let's see how this plays out for the function in the previous example:
|
Example
Find (again) the area under $f(x) = -x^2+4x$ and above the $x$-axis between $x=0$ and $x=4$. Solution Imagine the area sliced up into thin horizontal strips and the approximating rectangles for each of these strips. In the diagram below, one of these approximating rectangles is shown in magenta. 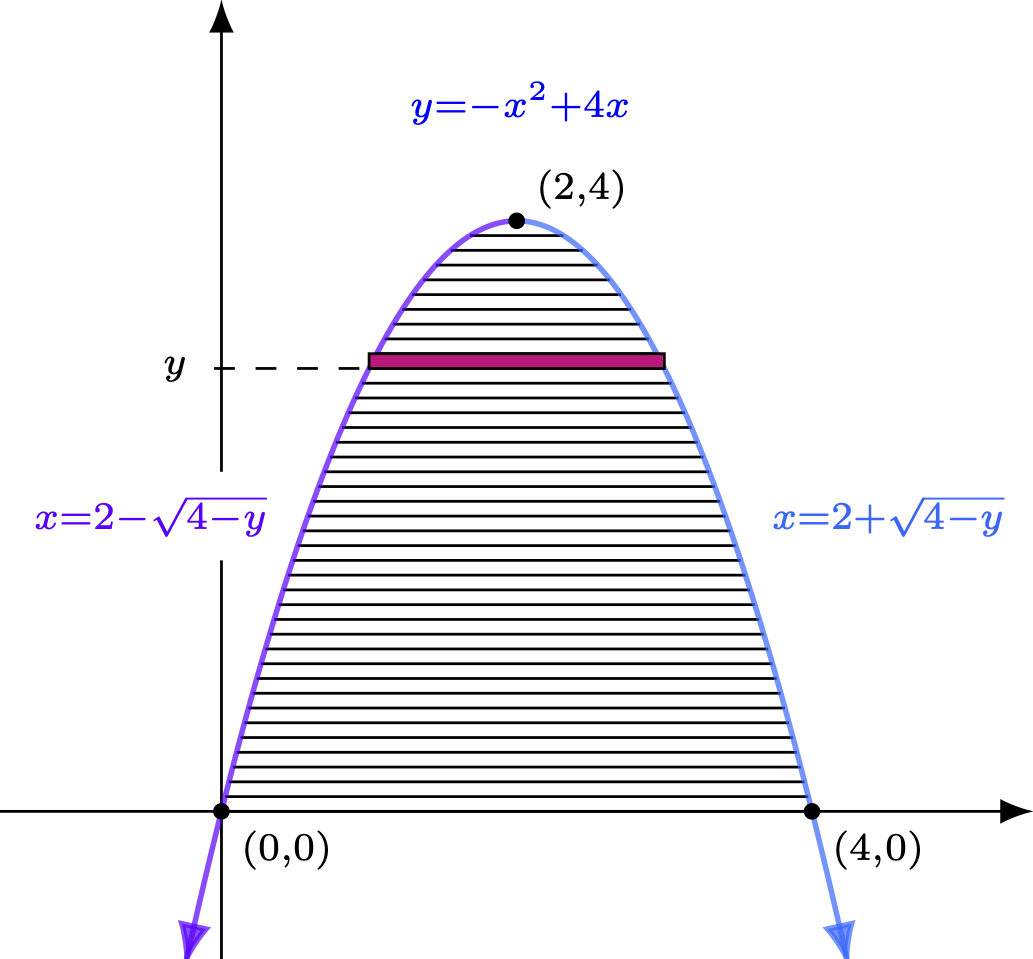 Note the width of the rectangle, being horizontal, is expressable as a difference of $x$-coordinates -- but unlike the previous example, this width is not the "small dimension" this time. As the rectangle spans the distance between the left and right sides of the parabola for some height given by $y$, we need to find the two $x$ values that correspond to this value of $y$. Fortunately, these are easy to find by solving the equation $y=-x^2+4x$ for $x$. There are two solutions, $x=2-\sqrt{4-y}$ and $x=2+\sqrt{4-y}$. Note that regardless of the height $y$ in question, the left $x$-coordinate of the rectangle at that height is always given by the former, while the right $x$-coordinate of the same is always given by the latter. When given two different $x$-coordinates, the one on the right is always the bigger one, so to find the distance between them, we subtract the left $x$-coordinate from the right one (to ensure we have a positive result). As such, the width of the rectangle is given by $$\begin{array}{rcl} \textrm{width of rectangle at height } y &=& (2+\sqrt{4-y}) - (2-\sqrt{4-y})\\ &=& 2\sqrt{4-y} \end{array}$$ The height of the rectangle, being vertical, is expressable as a difference of $y$ coordinates. Assuming a regular partition, we can call this height $\Delta y$. At this point, we could setup an associated Riemann sum that would lead to the definite integral sought. For completeness, this is given below -- but one can be more efficient by thinking about how the same pieces of information that go into the construction of the Riemann sum can be used to build the definite integral directly. $$\sum_{i=1}^n \underbrace{\left[2\sqrt{4-y_i^*}\right]}_{\textrm{width}} \, \underbrace{\Delta y}_{\textrm{height}}$$ To bypass the construction of the Riemann sum, recall that as we take a limit as $\lVert \Delta y \rVert \rightarrow 0$, this factor effectively turns into the $dy$ in the definite integral we are constructing. Thus, the area of the rectangle at height $y$ is given by $$\underbrace{2 \sqrt{4-y}}_{\textrm{width}} \, \underbrace{dy}_{\textrm{height}}$$ Putting this together with the fact that we only wish to consider the area contributions of the approximating rectangles at heights between $y=0$ and $y=4$ (which provide the limits of integration), we have the area under $f(x)$ and above the $x$-axis given by $$\int_0^4 2\sqrt{4-y}\,dy$$ Of course, now we can apply the fundamental theorem of calculus to evaluate this area. Provided we have done everything correctly, of course, we should get the exact same area as found in the first example since it is the same region of the plane that we are talking about after all! $$\begin{array}{rcl} \displaystyle{\int_0^4 2\sqrt{4-y}\,dy} &=& \displaystyle{\left.\left(-\frac{4}{3} (4-y)^{3/2}\right)\right|_0^4}\\ &=& \displaystyle{0 - \left(-\frac{4}{3} \cdot 8 \right)}\\ &=& \displaystyle{\frac{32}{3}} \end{array}$$ Woo Hoo! We got the same area! |
The two examples above tell us that when we are trying to find an area using a definite integral, there may be multiple ways we can proceed. For the particular region explored in these two examples, the definite integral produced by considering horizontal strips was slightly more difficult to produce than the one resulting from considering vertical strips (recall we had to solve for $x$ in terms of $y$ only in the horizontal case). For other regions, we might have the reverse -- using horizontal strips might be easier than using vertical ones. The moral of the story is to think carefully about what is required and how much work must be done to setup the related definite integrals. Then, pick the easiest route!
Of course, we need not restrict our attention to finding areas solely under a single function and above the $x$-axis. As we see next, we can use the same ideas found in the examples above to find areas bound by more than one curve as well!
|
Example Find the area bound between the graphs of $y=2x^2+10$ and $y=4x+16$ Solution First, we will want to graph both curves. The first is an upwards-opening parabola with $y$-intercept of $(0,10)$. The second is a line of positive slope whose $y$-intercept is higher, at $(0,16)$. Drawing these will give us a good idea of the general shape of the region bound between them -- but to get an even better representation, let us also find out where these curves intersect. We do this in the normal way, setting the right-hand sides equal and solving for $x$: $$\begin{array}{rcl} 2x^2+10 &=& 4x+16\\ 2x^2-4x-6 &=& 0\\ x^2-2x-3 &=& 0\\ (x+1)(x-3) &=& 0\\ x &=& -1 \textrm{ or } 3 \end{array}$$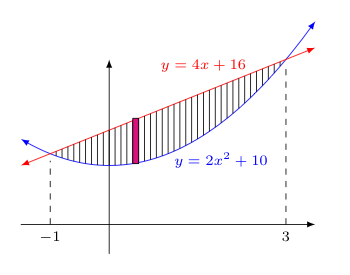 In addition to graphing both curves, notice we have sliced the area bounded between these two functions into vertical strips -- highlighting one of these strips with its approximating rectangle, colored magenta. Think about the area the magenta rectangle contributes to the Riemann sum that approximates the area between the curves. This rectangle's width (a horizontal distance) is some small difference of $x$-coordinates -- a $\Delta x$. It's height (a vertical distance) is the difference of a $y$-coordinate on the upper (red) function and the corresponding $y$-coordinate on the lower (blue) function. As such, $$\begin{array}{rcl} \textrm{height of rectangle at $x$ } &=& (4x+16) - (2x^2+10)\\ &=& -2x^2 + 4x + 6 \end{array}$$ for some $x$ in the interval $[-1,3]$. Importantly, as the above demonstrates, notice that we always find a vertical distance between two points with different $y$ values by subtracting the lower $y$-coordinate from the higher one, so that the difference (which represents a distance) yields a positive value. Multiplying the height and width together for each such rectangle, the sum of the areas of the approximating rectangles for the strips shown can of course be represented by a Riemann sum of the form $$\sum_{i=1}^n \left[-2(x_i^*)^2+4(x_i^*)+6)\right] \Delta x$$Setting up the definite integral directly (shown below) is more efficient though. $$\int_{-1}^3 [-2x^2+4x+6]\,dx$$From this point, finding the area is routine -- we simply find an antiderivative and appeal to the Fundamental Theorem of Calculus to evaluate the definite integral: $$\begin{array}{rcl} \textrm{Area } &=& \displaystyle{\int_{-1}^3 [-2x^2 + 4x + 6]\,dx}\\ &=& \displaystyle{\left( -\frac{2}{3}x^3 + 2x^2 + 6x \right) \bigg\rvert_{-1}^3}\\ &=& \displaystyle{\frac{64}{3}} \end{array}$$ |
Notice again, in the above example, the "small dimension" of the rectangles involved was a tiny change in the $x$-coordianates, which then showed up in the Riemann sum as a $\Delta x$, and ultimately in the definite integral as a $dx$.
As discovered earlier, there are often other options for how to "slice up" our area. The next example shows how we could find an area by "slicing it up" either into rectangles whose small dimension is representable as a $\Delta x$ (i.e., thin vertical rectangles) or as a $\Delta y$ (i.e., thin horizontal rectangles) -- and thus can be computed either with a definite integral in terms of $x$, or a definite integeral in terms of $y$.
|
Example Find the area bound by the curves $y=x^2$ and $y=-x^2 + 4x$ in two different ways. Solution As before, we will want to first graph both functions (which both graph as parabolas down) and find any points of intersection. To graph the parabolas, we observe the first has a vertex at $(0,0)$ and opens up, while the secondopens down and can be rewritten (by completing the square) as $$\begin{array}{rcl} y &=& -(x^2-4x)\\ &=&-(x^2-4x+4)+4\\ &=&-(x-2)^2+4 \end{array}$$ and thus has a vertex at $(2,4)$. Finding points of intersection in the normal way, we discover $$\begin{array}{rcl} x^2 &=& -x^2 + 4x\\ 2x^2 - 4x &=& 0\\ 2x(x-2) &=& 0\\ x &=& 0 \textrm{ or } 2 \end{array}$$ Nicely, the intersections then just happen to be at the vertices earlier found. Thus, graphing them together we have 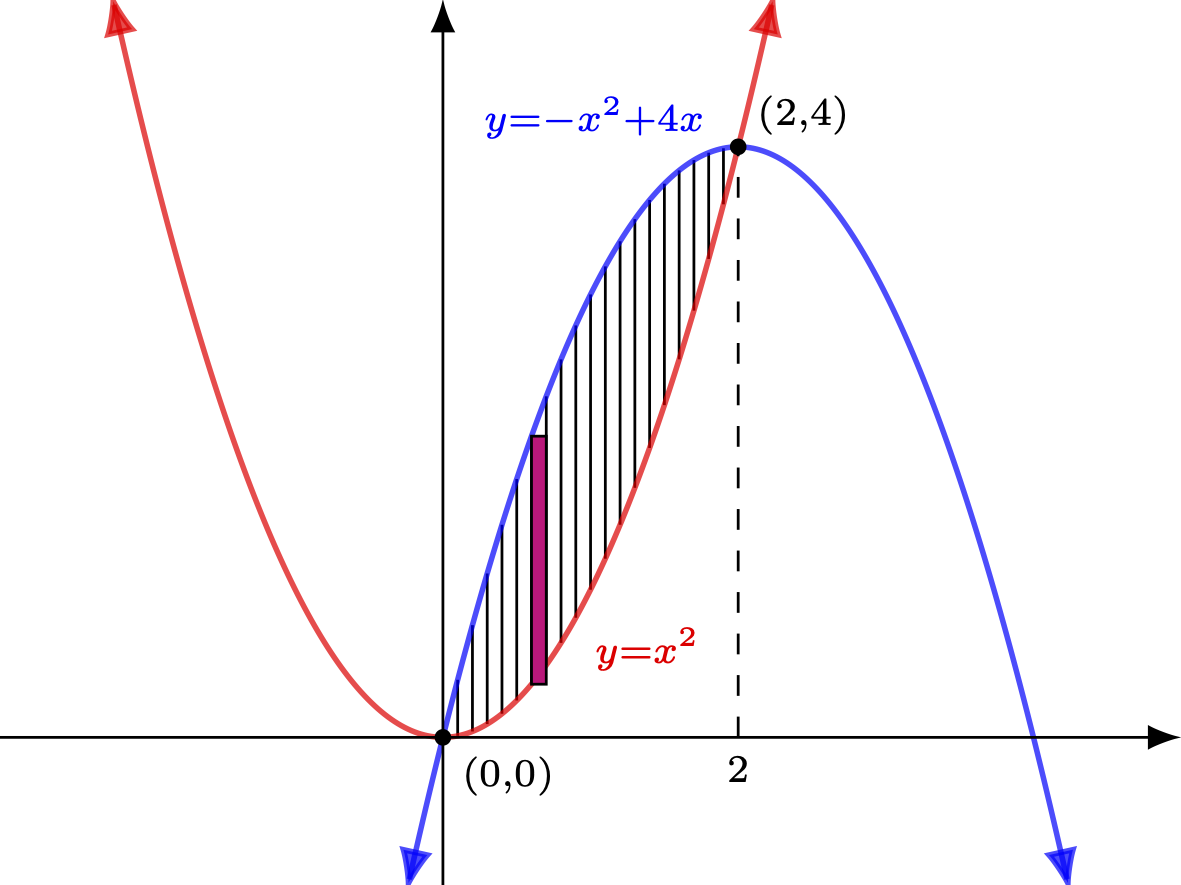 As was done in the first example, if we slice the bounded area vertically into roughly rectangular strips, we make the width (a horizontal distance) of each of the approximating rectangles a small $\Delta x$, which will eventually turn into a $dx$ in a definite integral that gives this area. Similarly, we find the height (a vertical distance) of each rectangle by subtracting the $y$-coordinate on the lower (red) function from the $y$-coordinate of the upper (blue) function. When expressed in terms of $x$ (so as to match our $dx$) this height will be given by $(-x^2 + 4x) - (x^2) = -2x^2 + 4x$, provided $x$ is in the interval $[0,2]$ (otherwise we get a negative distance as the height). The area can thus be approximated by the following Riemann sum with a regular partition. $$\sum_{i=1}^n \left[(-(x_i^*)^2+4(x_i^*)) - (x_i^*)^2\right] \Delta x$$ We can just as quickly set up the similarly-structured definite integral that gives the exact area. $$\int_0^2 \left[-2x^2 + 4x\right] dx$$ Computing the value of this integral is straight-forward: $$\left. \left(- \frac{2}{3}x^3 + 2x^2 \right) \right|_0^2 = \frac{8}{3}$$ However, what if we slice the area bound by these curves horizontally instead? This is shown below. 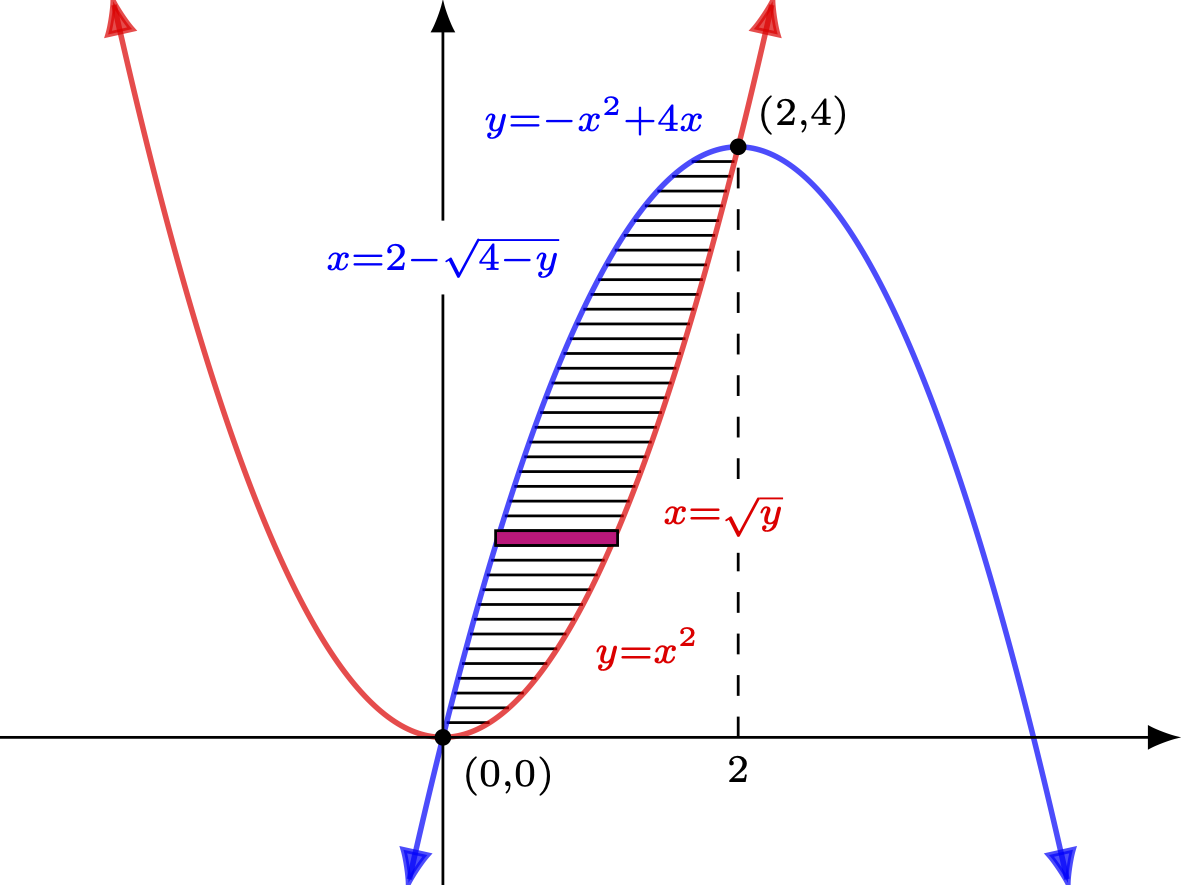 Notice the small dimension of each of the approximating rectangles is now a vertical distance/height and thus a difference of $y$-coordinates -- a $\Delta y$. One might be curious about the addition above of solutions for $x$ in terms of $y$ for both equations in question. The reason for their inclusion is this: for a given $y$-coordinate, if we find the approximating rectangle's width (a horizontal distance, and thus a difference in $x$ coordinates) in terms of $y$, we will be able to setup a Riemann sum using a (regular) partition of size $n$ of an appropriate $y$-interval that approximates the bound area. Then, taking a limit as $n \rightarrow \infty$, we can find the area bound by the curves as a definite integral in terms of $y$. Remembering to subtract the left (blue) $x$-coordinate from the right (red) $x$ coordinate so that the resulting horizontal width is positive, we can express the aforementioned limit of a Riemann sum as $$\lim_{n \rightarrow \infty} \sum_{i=1}^n \left[\left(\sqrt{y_i^*}\right) - \left(2 - \sqrt{4-y_i^*}\right)\right] \Delta y$$ which then becomes the definite integral given by $$\int_0^4 \left[\left(\sqrt{y}\right) - \left(2 - \sqrt{4-y}\right)\right] dy$$ Again, the computation of this definite integral is straight-forward and unsurprisingly results in $\frac{8}{3}$ once more. |
In some cases, now matter how we "slice" up our area sought, we can't calculate the "long" dimension of our rectangles in a consistent way. Often, this is due to two boundary curves crossing. When this happens, we will likely find the following property of definite integrals very useful:
For any integrable function $f(x)$: $$\int_a^b f(x)\,dx + \int_b^c f(x)\,dx = \int_a^c f(x)\,dx$$ We'll explore how this property can be used to deal with such a crossing in the next example.
|
Example Find the area between $y=\sin x$ and $y=\cos x$ from $x=0$ to $x=\pi/2$. Solution First, we graph the two functions over the interval in question, noting they intersect. We can find the point of intersection either by solving $\sin x = \cos x$ in this interval. Being familiar with the unit circle quickly leads to an intersection at $(\frac{\pi}{4},\frac{\sqrt{2}}{2})$. 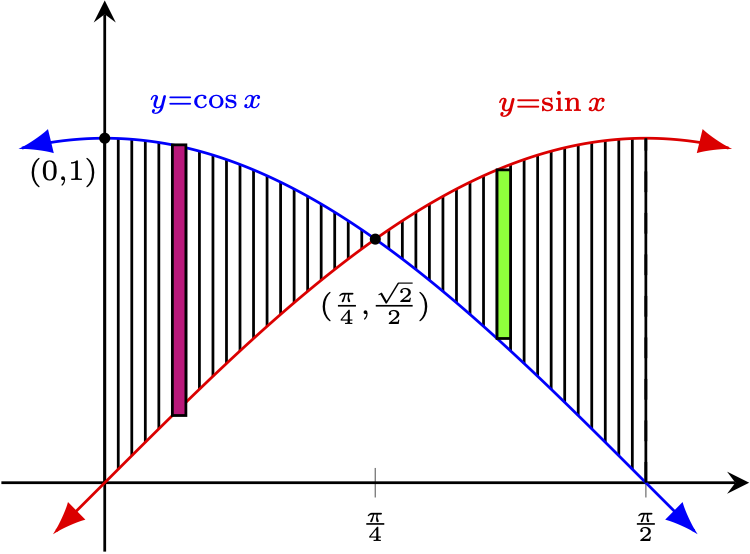 Slicing up the area vertically produces the strips shown above. The "small" dimension for all the resultant rectangles is then a horizontal distance -- a $\Delta x$ in the Riemann sum, which leads to a $dx$ in the definite integral. With $x$ established as the variable of integration, we seek to find the heights of the approximating rectangles in terms of $x$. Being a vertical distance, we must subtract the lower $y$-coordinate from the upper $y$-coordinate for each (so as to keep the resultant value positive, as all distances must be). However, for rectangles to the left of $x=\frac{\pi}{4}$ versus rectangles to the right of this value, these heights must be calculated differently! Notice for the magenta rectangle, which is representative of all the rectangles left of the intersection point, we see a height of $\cos x - \sin x$. For the green rectangle (representative of all the rectangles to the right of the intersection), the upper/lower functions have switched, meaning we must calculate the height with $\sin x - \cos x$ instead! As such, if $h(x_i^*)$ is the height of the $i^{th}$ rectangle as it appears in the Riemann sum, $h$ would be the piecewise-defined function: $$h(x) = \left\{ \begin{array}{l} \cos x - \sin x, \quad x \le \frac{\pi}{4}\\ \sin x - \cos x, \quad x \gt \frac{\pi}{4} \end{array} \right.$$ Rightfully wanting to avoid the difficulties that will create in either dealing with the Riemann sum or the definite integral with which it is associated, we can make our lives much simpler by remembering the property of definite integrals mentioned just before we started this example. Namely, for integrable functions $f$, $$\int_a^c f(x)\,dx = \int_a^b f(x)\,dx + \int_b^c f(x)\,dx$$ We need to integrate from $x=0$ to $x=\pi/2$, so these will play the roles of $a$ and $c$ above. Noting $\pi/4$ lies between them, we select this value to play the role of $b$. Doing so tells us the area can be expressed as the sum of two definite integrals: $$\int_0^{\pi/4} (\cos x - \sin x)\,dx + \int_{\pi/4}^{\pi/2} (\sin x - \cos x)\,dx$$ From there, finding the area is routine. We simply evaluate the definite integrals and add them together: $$\begin{array}{rcl} \displaystyle{\int_0^{\pi/4} (\cos x - \sin x)\,dx} &=& \displaystyle{\left(\sin x + \cos x\right)\biggr|_0^{\pi/4}}\\ &=& \left(\frac{\sqrt{2}}{2} + \frac{\sqrt{2}}{2}\right) - \left(0 + 1\right)\\ &=& \sqrt{2} - 1 \end{array}$$ $$\begin{array}{rcl} \displaystyle{\int_0^{\pi/4} (\sin x - \cos x)\,dx} &=& \displaystyle{\left(-\cos x - \sin x\right)\biggr|_{\pi/4}^{\pi/2}}\\ &=& \left(-1 - 0\right) - \left(-\frac{\sqrt{2}}{2} - \frac{\sqrt{2}}{2}\right)\\ &=& \sqrt{2} - 1 \end{array}$$ with the sum of these being the area sought: $$\textrm{Area } = 2(\sqrt{2} - 1)$$ An Alternate Solution (shorter, but not as generally applicable) Often, the only way to deal with an area associated with crossing functions is to do what we did above. However, in this particular problem, whose area sought just happens to be symmetric with respect to the vertical line $x = \pi/4$, we could significantly shorten our work by realizing the second integral has to agree in value with the first due to this symmetry. As such, we could just evaluate one of the definite integrals (either will suffice) and double its value! |
Let's consider one final example where more than one definite integral is necessary to find a given area.
|
Example Express the area enclosed by $y=\frac{x^3}{4}$, $y=-\frac{x}{4}$, and $y=-\frac{3}{2}x + 5$ in two ways -- one should involve "$dx$" and the other should involve "$dy$". Solution First, let's graph the region to get a better feel for it. Two of the bounding functions are linear, with the third being a simple cubic, so one should be able to graph all of these quite quickly. We will want to find the coordinates of any ponts of intersection as well. The intersection of the cubic and the $y=-x/4$ (the blue curve below) should be obvious, and finding the intersection of the two linear functions should be routine. Only the intersection of the other two functions proves interesting. Here, we set the $y$ values equal, eliminate the fractions, and then bring everything to one side to find $$\begin{array}{rcl} \frac{x^3}{4} &=& -\frac{3}{2}x+5\\ x^3 &=& -6x + 20\\ x^3 + 6x - 20 &=& 0 \end{array}$$ Factoring the left side is not obvious, so we cross our fingers that the solutions are rational and apply the rational root theorem. Recall this tells us that any solution that exists, if rational, will be expressible as a factor of the constant term over a factor of the leading coefficient. Notably, the graphs of the functions involved make it clear we should expect only one real solution. Further, the graphs suggest this sole intersection happens where $x>0$, so we need not worry about any negative factors. As the leading coefficient is $1$, we only need to consider $x=1,2,4,5,10$, and $20$. We set about evaluating $x^3+6x-20$ for each of these in turn, but stop as soon as we see $2$ is a solution. Once we know the intersection occurs at $x=2$, finding its $y$-coordinate is trivial. We simply find $\sqrt[3]{4 \cdot 2} = 2$. With all the intersections now found, and in anticipation of having to set up both integrals in terms of "$dx$" and "$dy$", let us label each curve with both the equation that gives $y$ in terms of $x$ (i.e., $y=f(x)$) and the equation that gives $x$ in terms of $y$ (i.e., $x = f^{-1}(y)$). 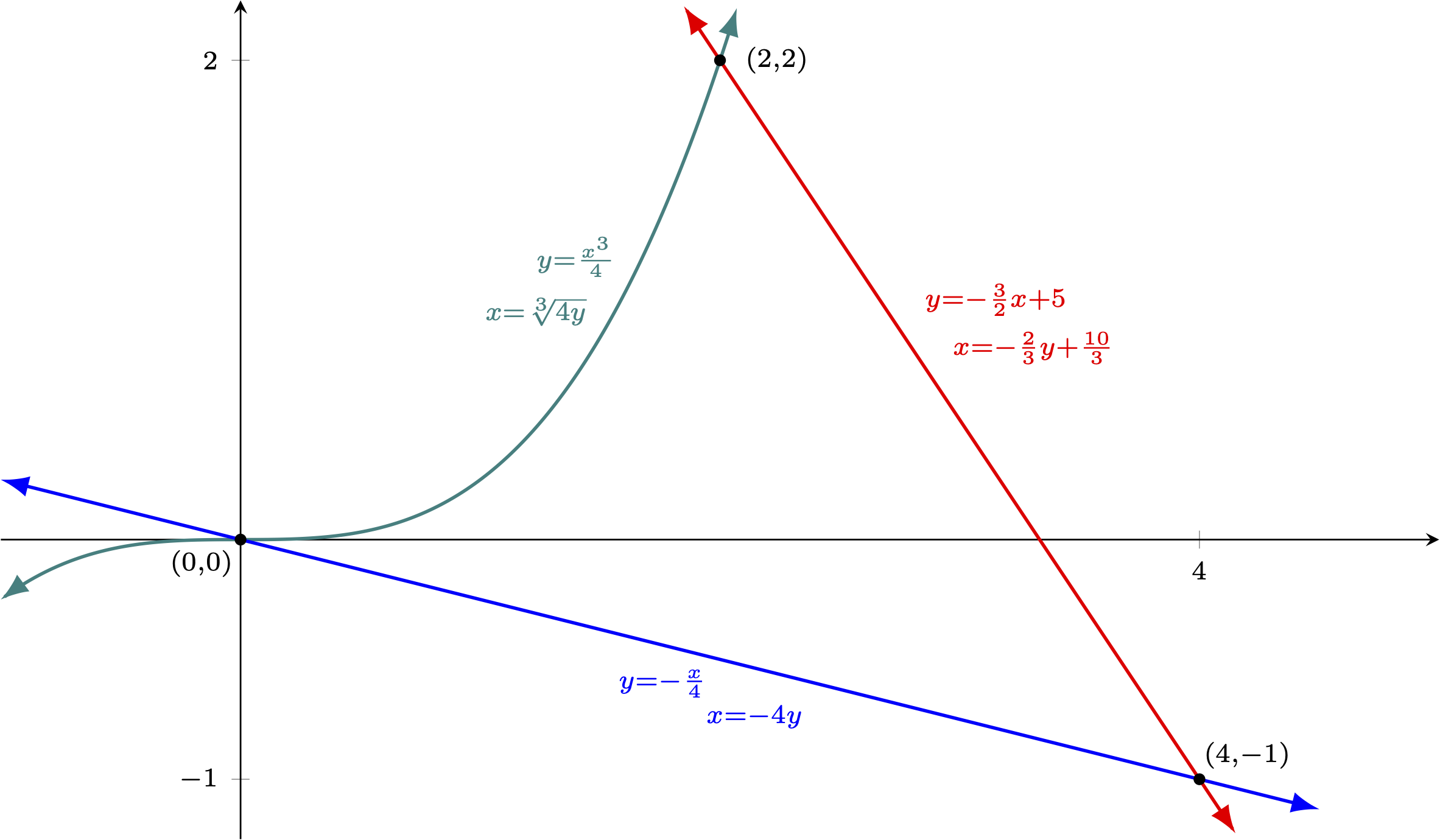 Considering how to find the area with definite integrals involving "$dx$" first, we realize that the "small" dimension of each approximating rectangle must be a difference of $x$ values and thus the tiny side of each rectangle is horizontal. This means that the area has been sliced into thin vertical strips. Note that the expression in terms of $x$ that will give the height of these rectangles changes depending on whether one is to the left of $x=2$ (where the green andred curves intersect) or to the right of this value. As such, we draw a representative approximating rectangle in each region and anticipate the area will thus be the sum of two definite integrals. 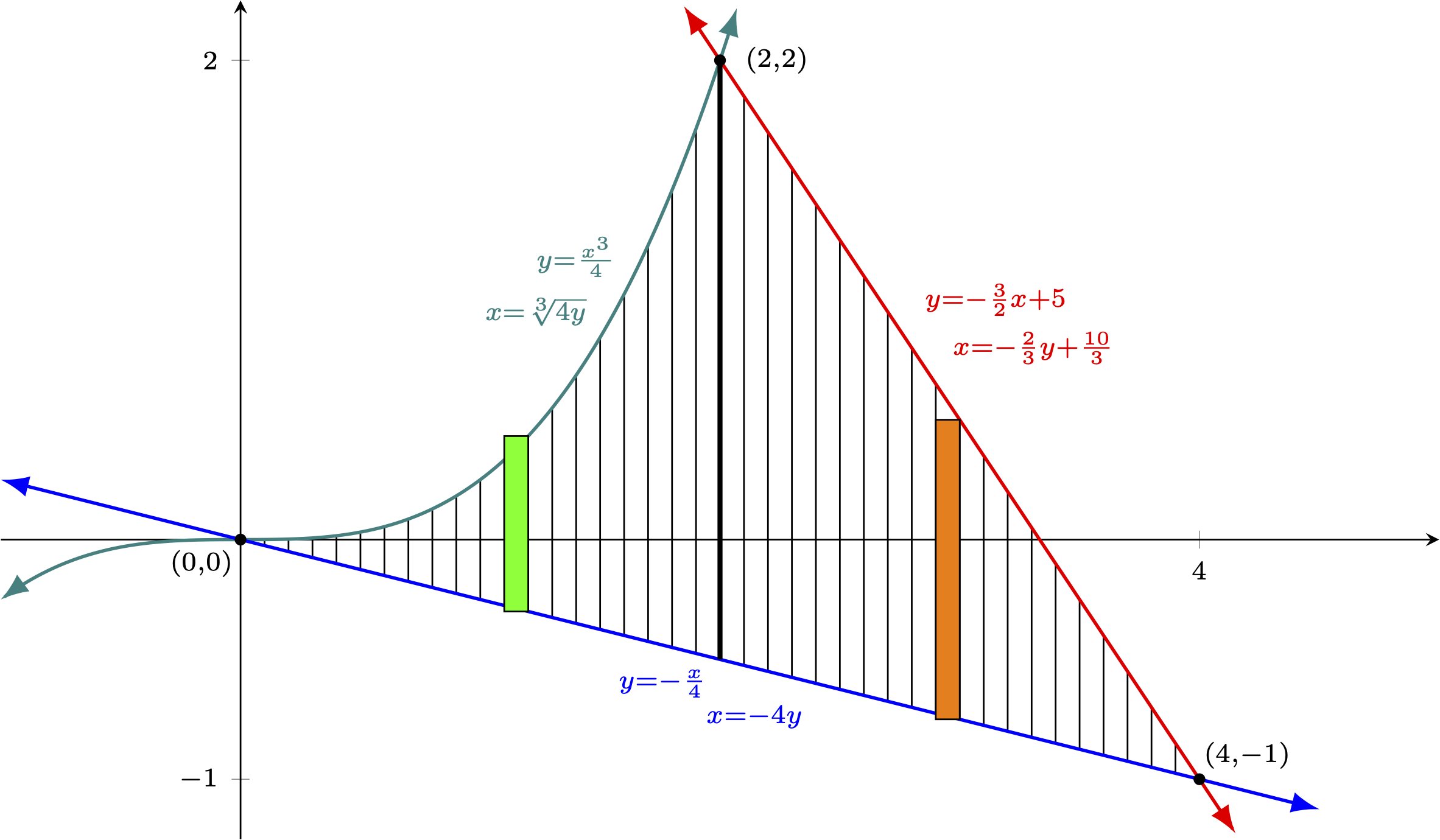 Remembering the heights of the rectangles are vertical distances and thus differences of $y$-coordinates, but must be found in terms of $x$ (to match the needed $dx$), we subtract the values of the $y$-coordinates in terms of $x$ for the green and blue curves to find the height of the light green rectangle, and the same for the red and blue curves to find the height of the orange rectangle. Recall we always subtract the lower $y$ from the upper one to ensure the result is positive and thus a reasonable value for a distance. $$\textrm{height of light green rectangle } = \frac{x^3}{4} - \left(-\frac{x}{4}\right)$$ $$\textrm{height of orange rectangle } = \left(-\frac{3}{2}x + 5\right) - \left(-\frac{x}{4}\right)$$ As all the approximating rectangles from $x=0$ to $x=2$ have heights found using the same expression as the one for the light green rectangle above, and all the approximating rectangles from $x=2$ to $x=4$ have heights found using the same expression as the one used for the orange rectangle, we now know the limits of integration on our two definite integrals, and can say $$\textrm{Area } = \int_0^2 \left[\frac{x^3}{4} - \left(-\frac{x}{4}\right)\right]\,dx + \int_2^4 \left[\left(-\frac{3}{2}x + 5\right) - \left(-\frac{x}{4}\right)\right]\,dx$$ The above gives the area in a way that involves "$dx$", as desired. (If you evaluate things, you should find the area is $4$. Make sure you can do this!) Turning our attention to expressing the area in a way that involves "$dy$" instead, we realize the "small" dimension of the rectangles used must each be a difference of $y$ values and thus the tiny side of each rectangle is vertical. This in turn means that the area has been sliced into thin horizontal strips, and we redraw our area as such. Note that the expression in terms of $y$ that will give the width of these rectangles changes depending on whether one is above or below the $x$ axis (given the intersection of the blue and green curves that happens at the origin). We again draw a representative approximating rectangle for each region (in light blue and brown, respectively), to help us focus on how to compute the related dimensions, and anticipate the area again being the sum of two definite integrals (but this time, in terms of "$dy$"). 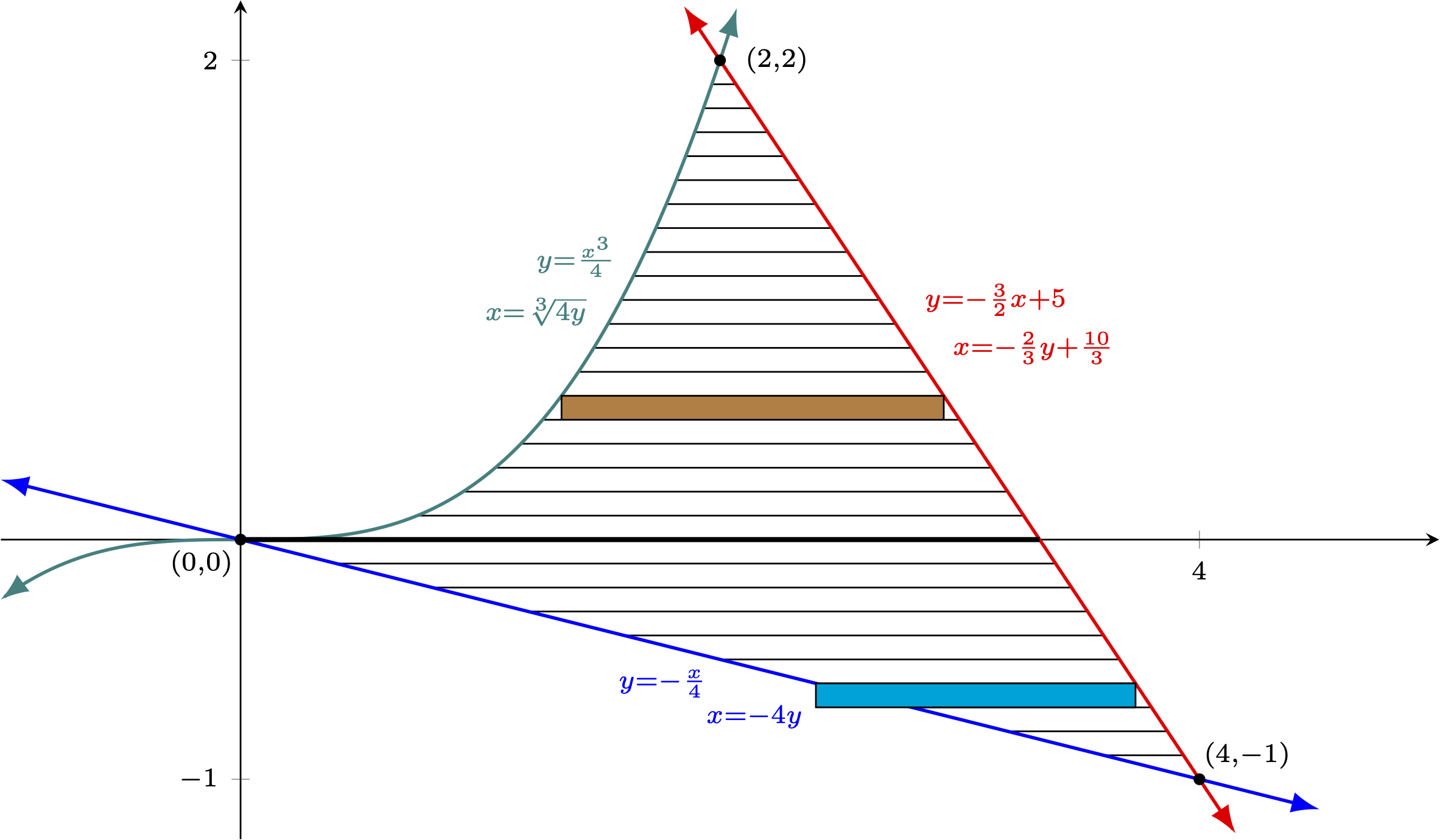 |