

 |  |
Thinking back to our intuitive notion of a limit, recall we said that barring any knowledge of what a function does at a particular $x$-value (as shown in the graph below when $x=2$), a limit can be thought of as an "expectation" for the height of the function at this $x$-value -- under an assumption that near this $x$-value, the graph of the function could be drawn with a single continuous stroke of a pen.
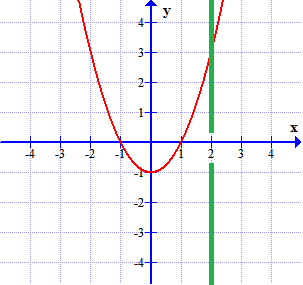
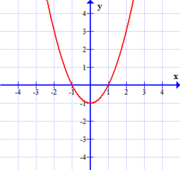
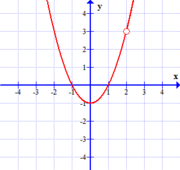
As we saw, this expectation, even if it exists, need not agree with the actual behavior of the function at the $x$-value in question. That is to say, it need not be that $\lim_{x \rightarrow c} f(x) = f(c)$. Consider the following three functions again.
 |
 |
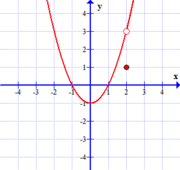 |
| $$f(x)=x^2-1$$ | $$f(x)=\frac{(x^2-1)(x-2)}{x-2}$$ | $$f(x)=\left\{ \begin{array}{cl} x^2-1 &\textrm{if } x \neq 2\\ 1 & \textrm{if } x = 2 \end{array} \right.$$ |
In the first example, the actual value of $f(2)$ agrees with our "expected value", $\lim_{x \rightarrow 2} f(x)$. Also note, that in the first example it appears the function can be drawn with a single continuous stroke of one's pen (around $x=2$, anyways).
In the second, $f(2)$ fails to even exist ($x=2$ is not in the domain of the second function), so there is no way it can agree with our "expected value", $\lim_{x \rightarrow 2} f(x)$. Also, it would appear that drawing this function requires us to momentarily lift the pen from the paper at $x=2$, given the "hole" there. As such, we can't draw this function with a single continuous stroke.
Likewise, in the third example, $f(2)$ exists, but disagrees in value with $\lim_{x \rightarrow 2} f(x)$. This again results in a "hole" in the function that causes us to lift our pen when attempting to draw this function. Consequently, we can't draw this function near $x=2$ with a single continuous stroke either.
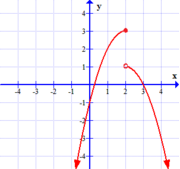
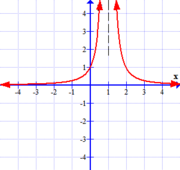
Similarly, if we look at three functions where the $\lim_{x \rightarrow c} f(x)$ fails to exist, we see in each case, functions that can't be drawn with a single continuous stroke of the pen around $x=c$. (Admittedly, the last function might be harder to follow -- but certainly you must agree that drawing this function around $x=0$ is difficult!)
 |
 |
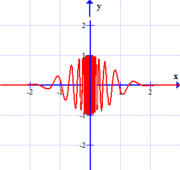 |
| $$y=f(x), \quad c=2$$ | $$y=g(x), \quad c=1$$ | $$y=h(x), \quad c=0$$ |
Of course, if $\lim_{x \rightarrow c} f(x)$ fails to exist -- we can't possibly have $\lim_{x \rightarrow c} f(x) = f(c)$.
So it would appear, from these examples, that we can only draw the graph of $y=f(x)$ near some $x=c$ in a single continuous stroke if three things happen:
$\lim_{x \rightarrow c} f(x)$ exists,
$f(c)$ exists (i.e., $c$ is in the domain of $f(x)$), and
$\lim_{x \rightarrow c} f(x) = f(c)$
Consequently, we say that $f(x)$ is continuous at $x=c$ if these conditions are satisfied.
Equivalently, given $\lim_{x \rightarrow c} f(x)$ exists if and only if $\lim_{x \rightarrow c^-} f(x)$ and $\lim_{x \rightarrow c^+} f(x)$ both exist and agree in value, we could also say $f(x)$ is continuous at $x=c$ if and only if $\lim_{x \rightarrow c^-} f(x)$, $f(c)$, and $\lim_{x \rightarrow c^+} f(x)$ ALL exist and agree in value.
There are lots of variations on a theme when it comes to the verbiage used in talking about continuous functions. For example:
We say that a function is continuous everywhere if it is continuous at every real value $c$.
We can also say that a function is continuous on its domain if it is continuous at every real value $c$ that falls in the domain of the function in question.
We say that a function is discontinuous at $x=c$ if any of the three conditions above fail to be true. Equivalently, we can say that $f(x)$ has a discontinuity at $x=c$.
We say that a function is continuous from the right at $x=c$ if $\displaystyle{\lim_{x \rightarrow c^+} f(x) = f(c)}$ and continuous from the left at $x=c$ if $\displaystyle{\lim_{x \rightarrow c^-} f(x) = f(c)}$.
Notice that functions can be discontinuous in a variety of ways (all but one of the small pictures above were discontinuous at some point).
If $\lim_{x \rightarrow c} f(x)$ exists, but for whatever other reason fails to be continuous at $x=c$ (i.e., either $f(c)$ doesn't exist or fails to equal the value of this limit), we say that $f(x)$ has a removable discontinuity at $x=c$.
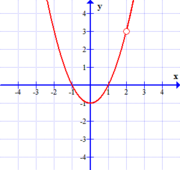
One can think of functions with removable discontinuities as being ones whose continuity is easily "repairable", in a certain sense. That is to say, if one simply defines (or redefines) the value of the function at $x=c$, the discontinuity can be removed. The following two graphs have removable discontinuities at $x=2$.
 |
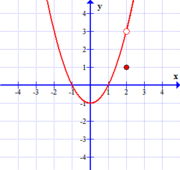 |
$$f(x)=\frac{(x^2-1)(x-2)}{x-2}$$ |
$$f(x)=\left\{ \begin{array}{cl} x^2-1 &\textrm{if } x \neq 2\\ 1 & \textrm{if } x = 2 \end{array} \right.$$ |
As can be seen above, removable discontinuities present themselves graphically as "holes" in functions.
Of course, if $\lim_{x \rightarrow c} f(x)$ does not exist, then defining or redefining the value of $f(x)$ at $x=c$ will not be sufficient to remove the discontinuity. We say in this situation that $f(x)$ has a non-removable discontinuity at $x=c$}.
Graphically, non-removable discontinuities present themselves in a variety of ways, two of which we give names to:
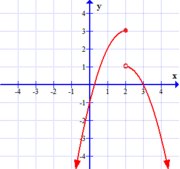
We say we have a gap or jump discontinuity when $\lim_{x \rightarrow c} f(x)$ does not exist due to the left and right limits existing, but disagreeing (i.e., $\lim_{x \rightarrow c^-} f(x) \neq \lim_{x \rightarrow c^+} f(x)$ (see graph D below)
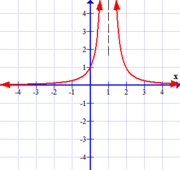
We say we have a vertical asymptote when $\lim_{x \rightarrow c} f(x)$, or one of its related one-sided limits does not exist because it is infinite. (see graph E below)
 |
 |
There are many examples of continuous functions. For example, consider a polynomial function $p(x)$. We know the domain of $p(x)$ is the set of all reals. This in combination with one of our limit laws, "$\lim_{x \rightarrow c} p(x) = p(c)$ whenever $p(x)$ is a polynomial function," tells us that $\lim_{x \rightarrow c} p(x)$ and $p(x)$ both exist and agree in value for every real number $c$. Thus, all polynomial functions are continuous everywhere (i.e., at any real value $c$).
With arguments like these (ones that appeal back to the limit laws for simple functions and combinations of functions), we can similarly deduce the following functions are continuous on their domains:
polynomial functions
rational functions (i.e., quotients of two polynomials)
odd root functions (i.e., $\sqrt[n]{x}$ for odd $n>1$)
Note: even root functions (i.e., functions of the same form as above, but where the aforementioned index $n$ is even instead of odd) are continuous on $(0,\infty)$ and continuous from the right at $x=0$.
trigonometric functions
inverse trigonometric functions
exponential functions
logarithmic functions
We can also appeal to the limit laws to discover that if functions $f$ and $g$ are continuous at some $x=c$, then the following combinations are as well:
$f+g$
$f-g$
$fg$
$kf$, where $k$ is some constant
$\displaystyle{\frac{f}{g}}$, provided $g(c) \neq 0$