• About
• Statistics
• Number Theory
• Java
• Data Structures
• Cornerstones
• Calculus

The Definition of the Derivative

Remember all our recent discussions regarding how to evaluate limits stemmed from the problem of determining tangent slopes to graphs of functions at particular points. Now that we have the ability to find all sorts of limits, we can return to this very important problem.

Recall, our strategy for finding the slope of the tangent line to the graph of some function $f(x)$ at some point $P$ was to consider the limiting slope of the secant line through $P$ and some nearby point $Q$ as $Q$ approaches $P$.

We can set up this limit in a couple of different ways, although they are completely equivalent to one another.

One Limit That Gives the Tangent Slope

Suppose the point $P$ is corresponds to the point on the graph of $f$ at $x=a$, and the point $Q$ is some nearby $x$-value, as shown below.

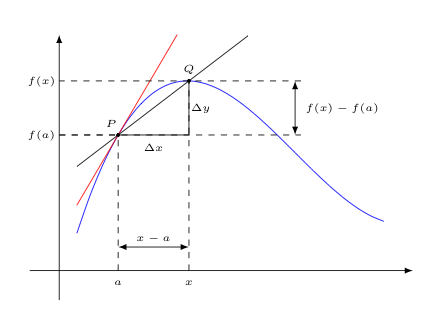
Since both $P$ and $Q$ are points on the graph of $f$, they then have coordinates $(a,f(a))$ and $(x,f(x))$, respectively.

Notice that the change in the $y$-coordinates, $\Delta y$ is then $f(x) - f(a)$, while the change in the $x$-coordinates, $\Delta x$ is $x-a$.

This means that the slope of the secant line, which is calculated as the "rise-over-run", $\displaystyle{\frac{\Delta y}{\Delta x}}$, is then given by

Now, recall we want the limiting slope value as the point $Q$ approaches $P$. Of course, this is equivalent to considering the limiting slope value as $x \rightarrow a$. As such, the slope of the tangent line at $x=a$ is given by

provided this limit exists.

If we change the value of $a$ in this limit, we get the slope of a different tangent line. In this sense, the expression above can be thought of as a function of $a$ that produces the slope of the tangent line to the point on the graph of $f(x)$ at $x=a$ (provided it exists).

This "tangent-slope producing" function is known as the derivative of $f$, and is denoted by $f'$.

Thus, given the above we can write the following provided the specified limit exists.

Provided this limit exists, we also say that $f$ is differentiable at $a$. As a variant, we say $f$ is differentiable on an interval if it is differentiable at each value in that interval. Alternatively, we may say $f$ is differentiable everywhere to mean that the derivative exists at all real numbers.

An Alternate (and Sometimes More Useful) Form

Note how in the above definition, we used an input of $a$ instead of the more typical $x$ that one generally associates with the input to a function -- how many times have you written $f(x)$ versus how many times have you written $f(a)$?

For most functions, we can easily write a definition for $f(x)$ from one for $f(a)$ by simply swapping out every $a$ in the definition for $f(a)$ with an $x$. As an example, if $f(a) = 2a^2 + \sin a$, then $f(x) = 2x^2 + \sin x$.

However, things are not as simple in our definition of the derivative of $f$, as we already have an $x$ being used in the definition! If we just replaced every $a$ with and $x$, we end up with a non-sensical limit where $x \rightarrow x$!

Thus, if we want to write $f'(x)$, we'll need to change the variable associated with the $x$-value of $Q$. A simple solution would be to just change the $x$s in the limit to some other letter, like $u$, and then change all the $a$s to $x$s -- however, there is something better we can do.

Consider the following limit:

Notice how we needed to factor the numerator, crossing our fingers that a common factor existed in the numerator and denominator, to evaluate the limit.

Now consider this other limit:

Notice how this last limit was much easier to evaluate, as it was clear an $h$ would cancel from the numerator and denominator. This ease comes from the fact that identifying common monomial factors is a lot easier than identifying common binomial factors. If a monomial factor in the denominator is present on every term in the numerator, you can cancel it. Done!

To see this advantage in our derivative limit, however, we'll need to let some variable (traditionally $h$) represent the difference between the $x$-coordinates of $P$ and $Q$. In this way $h$ now plays the role of $x-a$.

Notably, we can then express $Q$ approaching $P$ not with $x \rightarrow a$, but rather with $h \rightarrow 0$.

Consider the image below, which is essentially identical to the image we used above that led to a definition for $f'(a)$, except the coordinates have been renamed. The old $a$ (the $x$-coordinate of $P$) is now $x$, as desired, and $f(a)$ consequently turns into $f(x)$. The old $x$ (the $x$-coordinate of $Q$) has been replaced by $x+h$, since $Q$ should be $h$ units away from $P$ (along the $x$-axis). This of course means that the old $f(x)$ also then turns into $f(x+h)$.

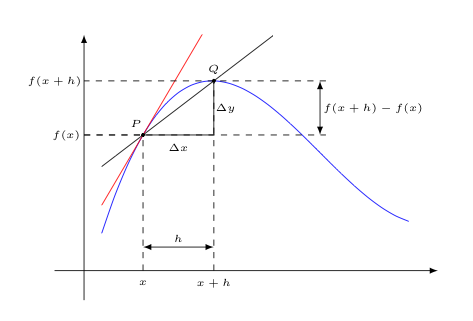
Now, in finding the slope of the secant line, the "rise" $\Delta y$, still being a difference of $y$-coordinates at $Q$ and $P$ is now $f(x+h) - f(x)$, while the "run" $\Delta x$, is more simply expressed as just $h$ (by design).

Thus, the limiting secant slope we seek is given by

As such, we may also (and in a completely equivalent way) define the derivative of $f$, denoted again by $f'$ by $$f'(x) = \lim_{h \rightarrow 0} \frac{f(x+h) - f(x)}{h}$$

presuming this limit exists.

As suggested by the above discussion, this form often (but not always) leads to limits that are slightly easier to evaluate.

A Bit of History (and its Effect on Notation)

Assuming that they truly did develop things independently, it should be no surprise that their notations for the derivative differed slightly.

Newton introduced the "prime-notation" for the derivative that was used in our above discussion, whereby $f'(x)$ denotes the derivative of $f$ at $x$. This notation emphasizes the connection to the function $f$ and has the advantage that it is quick to write.

Leibniz emphasized something different with his notation. Recall that the derivative is a limiting value of a slope -- a "rise over run" where the "rise" is the change in $y$-values $\Delta y = f(x+h)-f(x)$ and the "run" is the change in $x$-values $\Delta x = (x+h) - x = h$.

Of course in the limit, we look at what happens when $\Delta x \rightarrow 0$. That is to say, $\Delta x$ is getting very small. Indeed, if the limit exists, then $\Delta y$ will need to get small too.

(Think about that for a minute -- what happens if $\Delta y$ doesn't approach zero when $\Delta x$ approaches zero? What would be the limiting value of $\Delta y/\Delta x$?)

Now for what will initially seem to be a random factoid: The symbol Delta, $\Delta$, which often represents some sort of change, whether in mathematics or other disciplines, is an upper-case letter of the Greek alphabet. The lower-case version of the same letter, $\delta$, looks not too disimilar from the Roman letter "d". This of course is no coincidence, as both letters correspond to the same sound.

To emphasize the "smallness" of $\Delta x$ and $\Delta y$ in the limit, Leibniz chose to use this "d", the lower-case Roman version of upper-case Greek $\Delta$, in the way he denoted the derivative of a function $y=f(x)$, writing

One of the advantages of Leibniz's notation over Newton's is that it makes explicit the independent and dependent variables involved. These need not always be $x$ and $y$. Remember, we can interpret slopes of tangent lines as instantaneous rates of change in a wide variety of contexts. How is $y$ changing the instant $x$ is some value? How is the position of a moving object $s$ changing at some instant $t$? How is the volume of water in a lake $V$ changing the instant its depth is $h$? The answers to these questions could, in Leibniz's notation be written as

The real power of this notation comes into play when one looks at problems where multiple such rates must be considered at the same time. These are typically called "related rates" problems, and will be explored a bit later in our study of calculus.

As a variation on a theme -- one that emphasizes the action of transforming a function $f(x)$ into its derivative, much like functions themselves transform some input into some output -- the following notation is also used to represent the derivative of $f(x)$:

As a quick example of using this alternate notation, if $f(x) = x^2+3$, the derivative of this function could be written as $\displaystyle{\frac{d}{dx}(x^2+3)}$.

We will often have a need to take a derivative of a derivative of a function, known as the second derivative, or a derivative of the second derivative, known as the third derivative. Even higher derivatives can and sometimes are taken. When taking $n$ successive derivatives of a function, the result is called the $n^{th}$ derivative of that function.

We abbreviate the second derivative with a notation inspired by the last variant discussed above on Leibniz's notation:

Similarly, for the third derivative:

and so on..

Newton's notation was extended to a much simpler notation for higher derivatives by Joseph Louis Lagrange (1736-1813). The second, third, and higher derivatives of $f(x)$ using this notation are represented by the following notations, respectively.