

 |  |
When the limit for the derivative of a function $f$ at some $x = c$, $\displaystyle{\lim_{x \rightarrow c} \frac{f(x)-f(c)}{x-c}}$ exists we say that $f$ is differentiable at $c$. Likewise, if this limit does not exist, we say that $f$ fails to be differentiable at $c$.
Of course, this limit can fail to exist in different ways -- as is true for any limit.
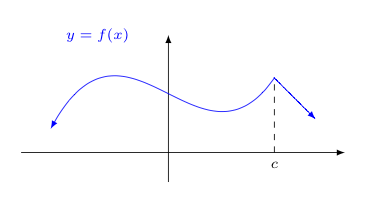
For example, the left and right limits could disagree. That is to say, $$\lim_{x \rightarrow c^-} \frac{f(x)-f(c)}{x-c} \ne \lim_{x \rightarrow c^+} \frac{f(x)-f(c)}{x-c}$$
Keeping in mind that the limit associated with the derivative represents a slope of a tangent line when it exists, the above suggests that the tangent slope coming in towards $x=c$ on the left and right differ. Graphically, this produces what is called a corner, as shown in the image below.
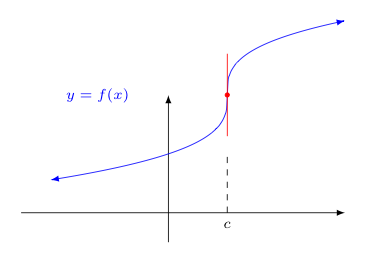
Another way the limit associated with $f'(c)$ could fail to exist would be if it were infinite. That is to say, if
$$\displaystyle{\lim_{x \rightarrow c} \frac{f(x)-f(c)}{x-c} = \pm \infty}$$Assuming for the moment that $f(c)$ exists, this means that the slope of the tangent line increases without bound as $x \rightarrow c$ (or decreases without bound in the case of $-\infty$). This means the graph of $f(x)$ has a vertical tangent line at $x=c$, as suggested by the image below.
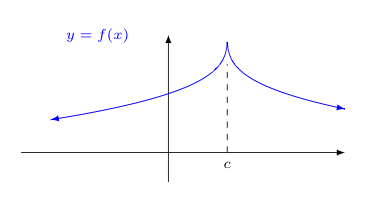
Of course, both of these issues could present themselves at the same time too. It might be the the left and right limits at $x=c$ are both infinite, but disagree (i.e., one is $+\infty$ while the other is $-\infty$). In this case, we have what is called a cusp in the graph at $x=c$. An example of what this looks like is shown below.
A more interesting way in which the limit associated with $f'(c)$ can fail to exist is for $f$ to be discontinuous at $x=c$. This is not immediately obvious, but easily proven.
Consider the limit in question
$$\lim_{x \rightarrow c} \frac{f(x) - f(c)}{x-c}$$For the moment, let us assume this limit exists.
Clearly, the denominator $x-c$ approaches $0$ as $x \rightarrow c$. This, however, requires the numerator approaches $0$ as $x \rightarrow c$ as well.
Think about the consequences otherwise. If the numerator approaches some $b \ne 0$ when $x \rightarrow c$, but the denominator becomes arbitrarily small, then the entire fraction grows in magnitude without bound. This in turn suggests the limit is infinite -- which technically means the limit does not exist. Thus, if the limit does exist, the numerator can't have a limiting value which is non-zero. Equivalently, if the limit exists, the numerator must have a limiting value of $0$.
As such, we know that
$$\lim_{x \rightarrow c} (f(x) - f(c)) = 0$$Applying the limit laws for the limit of a difference and the limit of a constant, we can then argue that
$$\lim_{x \rightarrow c} (f(x) - f(c)) = \lim_{x \rightarrow c} f(x) - \lim_{x \rightarrow c} f(c) = \left[\lim_{x \rightarrow c} f(x) \right] - f(c) = 0$$Focusing on the equality of the last two expressions above, let us add $f(c)$ to both to obtain
$$\lim_{x \rightarrow c} f(x) = f(c)$$This, of course, is precisely what we mean by $f$ being continuous at $x=c$.
We have hence proven the following important theorem:
| Theorem: If $f(x)$ is differentiable at $c$, then $f$ must also be continuous there. |
Now flip that result around. It must then also be the case that if $f$ is discontinous at $x=c$, then $f$ can not possibly be differentiable there.