

 |  |
Consider the graph of the function $\displaystyle{f(x) = x + \frac{1}{(x-2)^2}}$ shown below.
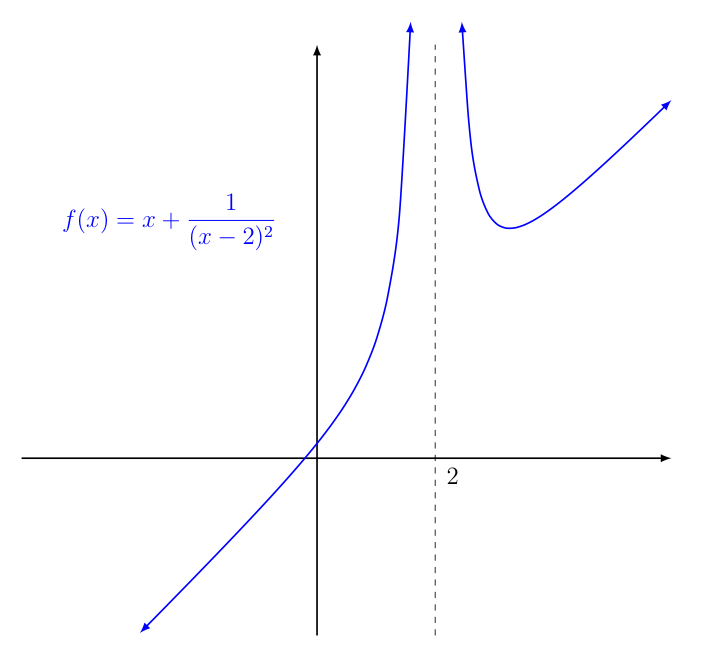
Notice how as $x \rightarrow 2$, it appears the function grows without bound.
We have previously said that we would write something like the following to describe this behavior:
$$\lim_{x \rightarrow 2} f(x) = +\infty$$As with all things in mathematics, however, we should be precise in what we mean when we write that a limit is infinite in this way (or is negative infinity, for that matter).
To this end, we look to how we have defined (finite) limits previously, for inspiration:
When we write $\lim_{x \rightarrow c} f(x) = L$ we mean that we can keep $f(x)$ arbitrarily close to $L$ (i.e., within some $\epsilon \gt 0$ of $L$) by keeping $x$ sufficiently close to $c$, with the possible exception of what happens at $x=c$.
So how does this play out when $L$ is replaced by $\infty$? What would we mean by "keeping $f(x)$ arbitrarily close to $\infty$"?
Well, infinity is not a number, so we can't talk about keeping $f(x)$ within $\epsilon$ units of it, like we do in the normal $\epsilon$-$\delta$ definition of a limit, but...
We do, however, have an intuitive feeling for one number being "closer" to infinity than another. For example, suppose you asked a fourth grader the question: "Which number is closer to infinity, 13 or 20 billion?'' They would probably say 20 billion, right? Why would they say this? Most likely they would say this because 20 billion is way larger than 13.
So let's use that idea. Let us replace the phrase "keep $f(x)$ arbitrarily close to $\infty$" with "keep $f(x)$ arbitrarily large".
That is to say, when we write $\displaystyle{\lim_{x \rightarrow c} f(x) = +\infty}$, we mean:
We can keep $f(x)$ arbitrarily large by keeping $x$ sufficiently close to $c$, with the possible exception of what happens at $x=c$.
Of course, there is a "less wordy" definition for an infinite limit that is more analogous to the epsilon-delta definition of a limit we have previously encountered.
The key to developing this is to realize that keeping $f(x)$ arbitrarily large is equivalent to being able to keep it larger than any value $N$ we might pick. Using this idea, we can write a formal definition for a (positive) infinite limit:
Formal Definition of a Positive Infinite Limit for $f(x)$ as $x$ approaches $c$ $\displaystyle{\lim_{x \rightarrow c} f(x) = +\infty}$ means that for any $N$ we can find a $\delta \gt 0$ such that $f(x) \gt N$ whenever $0 \lt |x - c| \lt \delta$. |
Of course, there is also the possibility that a function might have a limit of $-\infty$. This, of course, is handled in an almost identical way:
Formal Definition of a Negative Infinite Limit for $f(x)$ as $x$ approaches $c$ $\displaystyle{\lim_{x \rightarrow c} f(x) = -\infty}$ means that for any $N$ we can find a $\delta \gt 0$ such that $f(x) \lt N$ whenever $0 \lt |x - c| \lt \delta$. |