

 |  |
Find the area bound between the curves $y=x^2$ and $y=-x^2+4x$ in two different ways.
Find the area between $y=\sin x$ and $y = \cos x$, from $x=0$ to $x=\frac{\pi}{2}$
Find the area enclosed by the curves $y=x^3$, $y=-x$, and $y=-6x+20$ in two different ways.
Find the area between $y=\cos x$ and the $x$-axis from $x=-\pi$ to $x=2\pi$.
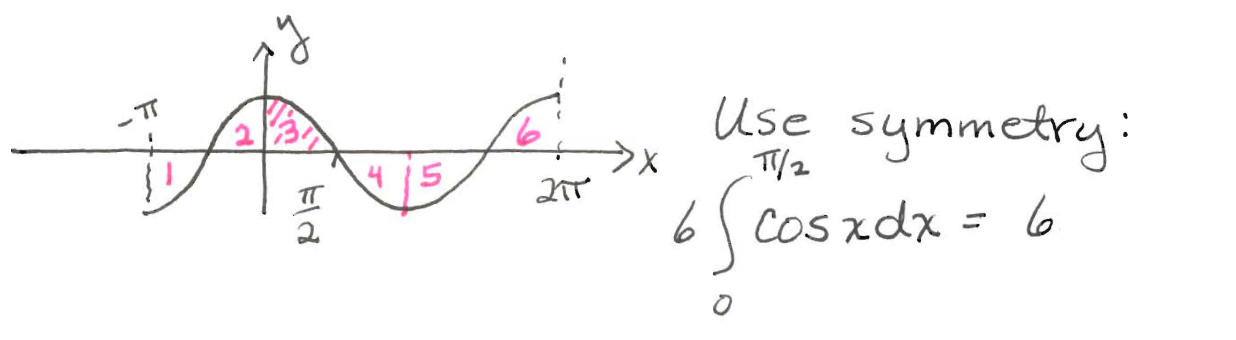
Find the area between $y=x^2-4x$ and the $x$-axis from $x=0$ to $x=6$.
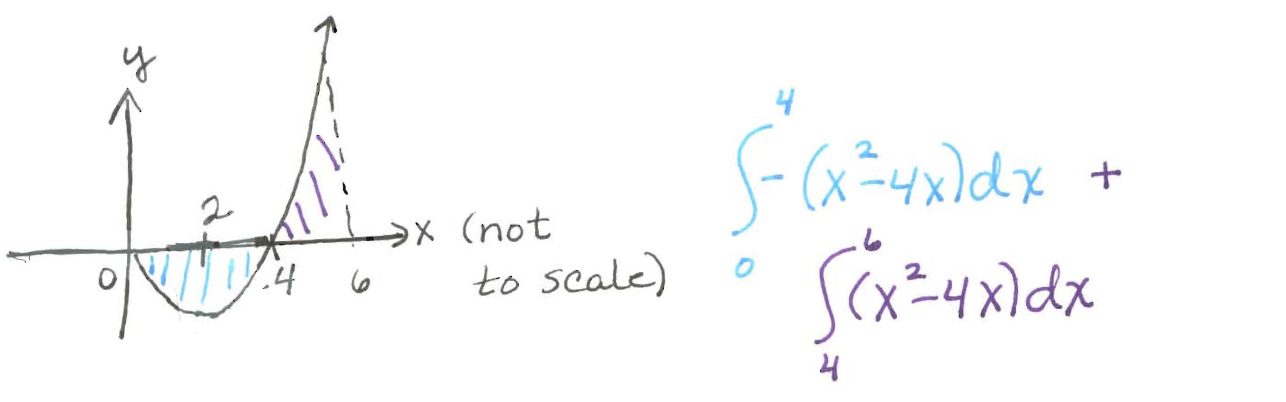
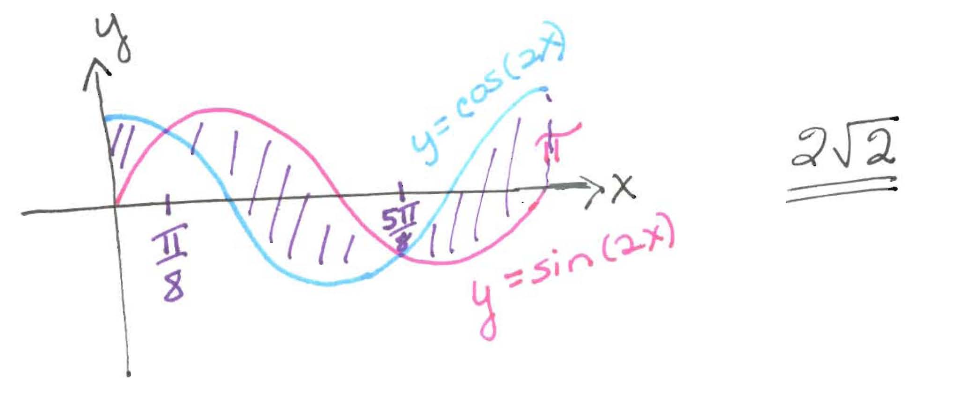
Find the area between $y=\sin 2x$ and $y=\cos 2x$ from $x=0$ to $x=\pi$.
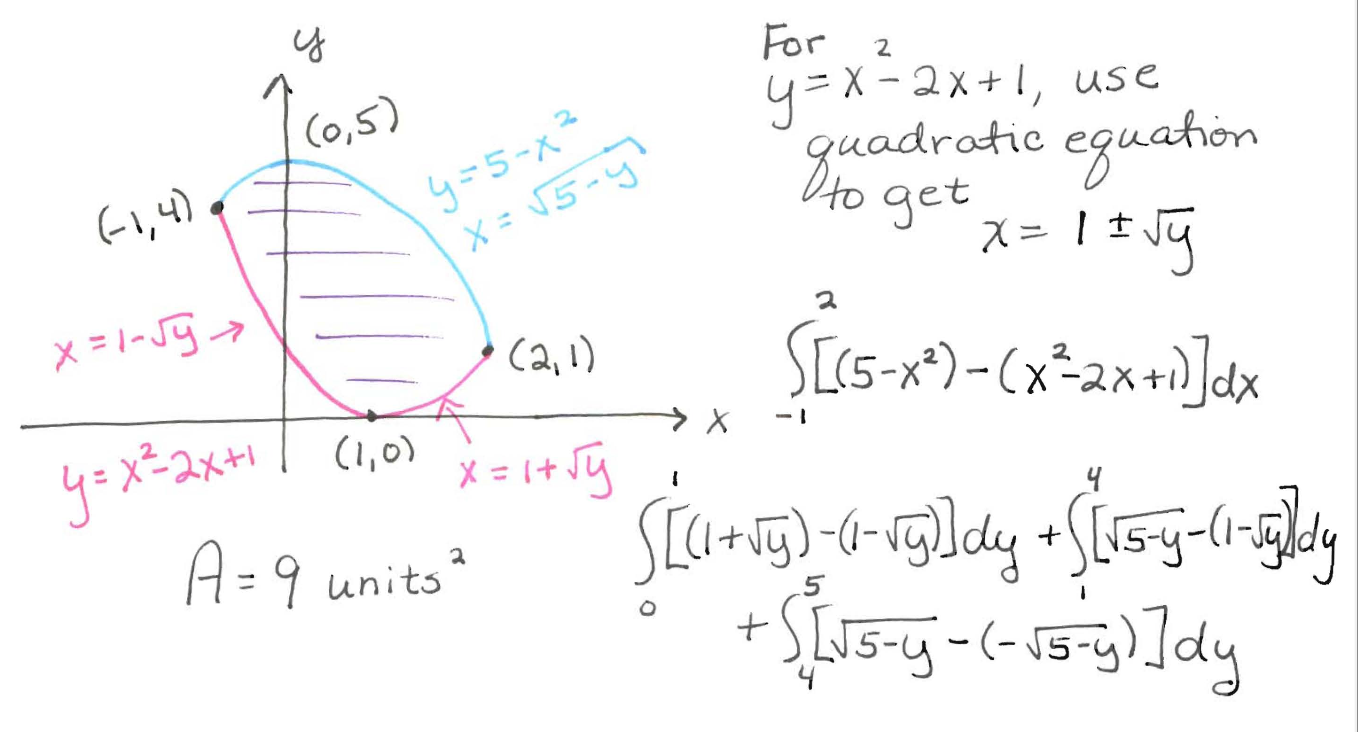
Sketch the graphs showing the region enclosed by $y=5-x^2$ and $y=x^2-2x+1$. Setup two expressions (one involving integral(s) in terms of $x$, the other involving integral(s) in terms of $y$) that will both give the area of the enclosed region. Find this area by evaluating one of these expressions.
Sketch the graphs showing the region enclosed by $y=x+4$ and $y=x^2-2$. Setup two expressions (one involving integral(s) in terms of $x$, the other involving integral(s) in terms of $y$) that will both give the area of the enclosed region. Find this area by evaluating one of these expressions.
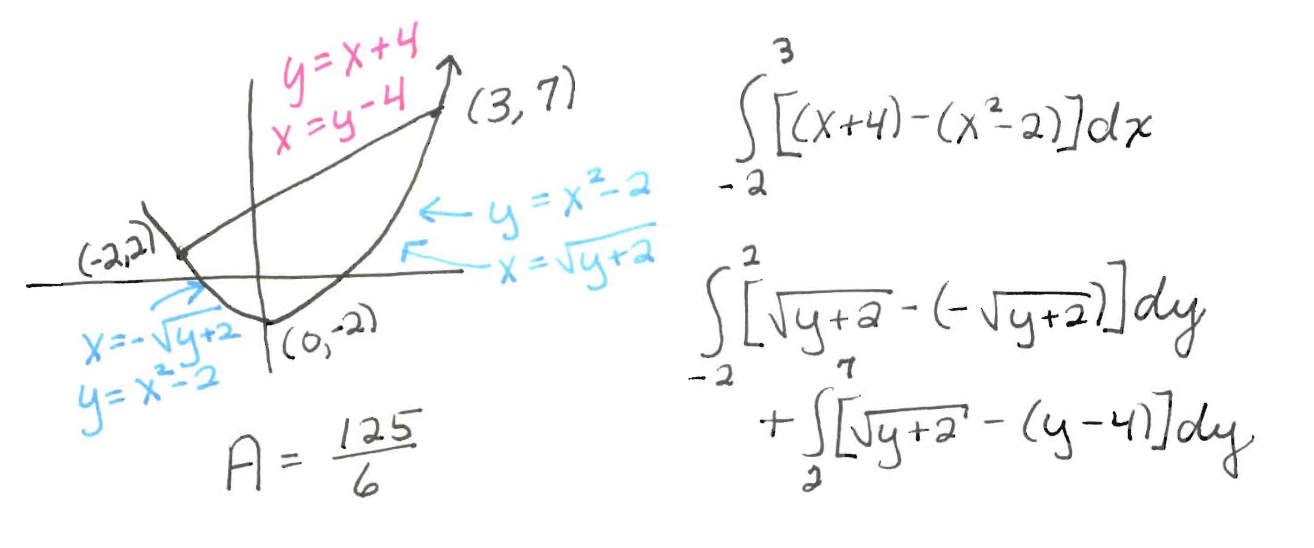
Find the area of the region between $y=x^2$ and $x-2y=2$ from $x=-2$ to $x=1$.
Find the area of the region bounded by $f(y)=y^2$ and $g(y)=4$.
Find the area of the region bounded by $x=3y+10$ and $x=y^2$ in two different ways (one involving integral(s) in terms of $x$, the other involving integral(s) in terms of $y$).
Find the area of the region bounded by $y=x^2-3x$ and $y=x$.
Find the area bounded by $x=y^2$ and $x=-y^2+2y+4$ in two different ways (one involving integral(s) in terms of $x$, the other involving integral(s) in terms of $y$).
Sketch the region enclosed by $y=x^2-2x$ and $y=-x^2+4$ and then setup the integral(s) necessary to find the area bound by these curves. Do this in two ways: one using integrals in terms of $x$; the other using integrals in terms of $y$.