

 |  |
Consider the following function,
$$f(x) = \left\{ \begin{array}{ll} -2x, & x \lt -1\\ |x|, & -1 \le x \lt 1\\ \displaystyle{\frac{1}{2-x}}, & x \ge 1 \end{array} \right.$$Find and classify all points where $f(x)$ is not differentiable.
We first seek any points where $f(x)$ has a discontinuity, as at these points $f(x)$ will not be differentiable.
The first two "pieces" (i.e, $-2x$ and $|x|$) are continuous everywhere, but the third (i.e., $1/(2-x)$) is not continuous at $x=2$ as this is the sole domain issue in this rational function.
At $x=2$: $$\lim_{x \rightarrow 2^-} \frac{1}{2-x} = +\infty$$ $$f(2) \textrm{ is undefined}$$ $$\lim_{x \rightarrow 2^+} \frac{1}{2-x} = -\infty$$
As the limits were infinite (and of different signs), $f(x)$ has an infinite, non-removable discontinuity in the form of a vertical asymptote at $x=2$, which then prevents $f(x)$ from being differentiable at $x=2$.
As $|x|$ is a piecewise-defined function in disguise, it may be helpful to rewrite $f(x)$ with the pieces of this function separated:
$$f(x) = \left\{ \begin{array}{ll} -2x, & x \lt -1\\ -x, & -1 \le x \lt 0\\ x, & 0 \le x \lt 1\\ \displaystyle{\frac{1}{2-x}}, & x \ge 1 \end{array} \right.$$This makes the "border values" (i.e., $-1$, $0$, and $1$) easier to see. Recall we must check all of these "border values", lest the function be discontinuous or not differentiable there as well.
At $x = -1$:
$$\lim_{x \rightarrow -1^-} f(x) = \lim_{x \rightarrow -1^-} -2x = 2$$ $$f(-1) = |-1| = 1$$ $$\lim_{x \rightarrow -1^+} f(x) = \lim_{x \rightarrow -1^+} |x| = 1$$As the left and right limits disagree, there is a non-removable gap discontinuity at $x=-1$, which prevents $f(x)$ from being differentiable at $x=-1$.
At $x = 0$:
$$\lim_{x \rightarrow 0^-} f(x) = \lim_{x \rightarrow 0^-} -x = 0$$ $$f(0) = 0$$ $$\lim_{x \rightarrow 0^+} f(x) = \lim_{x \rightarrow 0^+} x = 0$$As the function value at $x=0$ and the left and right limits there all agree, we know that $f(x)$ is continuous at $x=0$. However, that doesn't necessarily mean it is differentiable there. We must ensure the left and right limits of the derivative at $x=0$ also exist and agree for this to be true.
Note that for $-1 \lt x \lt 0$, we have
$$f'(x) = \lim_{h \rightarrow 0} \frac{f(x+h)-f(x)}{h} = \lim_{h \rightarrow 0} \frac{-(x+h)-(-x)}{h} = \lim_{h \rightarrow 0} \frac{-h}{h} = \lim_{h \rightarrow 0} -1 = -1$$Similarly, for $0 \lt x \lt 1$, we have
$$f'(x) = \lim_{h \rightarrow 0} \frac{f(x+h)-f(x)}{h} = \lim_{h \rightarrow 0} \frac{(x+h)-x}{h} = \lim_{h \rightarrow 0} \frac{h}{h} = \lim_{h \rightarrow 0} 1 = 1$$As these limiting values of the derivative exist but disagree, we have a corner at $(0,0)$ in the graph of $f(x)$, which is a point of non-differentiability.
At $x = 1$:
$$\lim_{x \rightarrow 1^-} f(x) = \lim_{x \rightarrow 1^-} |x| = 1$$ $$f(x) = \frac{1}{2-1} = 1$$ $$\lim_{x \rightarrow 1^+} f(x) = \lim_{x \rightarrow 1^+} \frac{1}{2-x} = 1$$As the function value at $x=1$ and the left and right limits there all agree, we know that $f(x)$ is continuous there. However, that doesn't necessarily mean it is differentiable there. We must ensure the left and right limits of the derivative at $x=1$ also exist and agree for this to be true.
We have already argued that for $0 \lt x \lt 1$, we have $f'(x) = 1$.
While for $x \gt 1$, we have
$$\begin{array}{rcl} f'(x) &=& \displaystyle{\lim_{h \rightarrow 0} \frac{\displaystyle{\frac{1}{2-(x+h)} - \frac{1}{2-x}}}{h}}\\\\ &=& \displaystyle{\lim_{h \rightarrow 0} \frac{(2-x)-(2-x-h)}{h(2-x-h)(2-x)}}\\\\ &=& \displaystyle{\lim_{h \rightarrow 0} \frac{h}{h(2-x-h)(2-x)}}\\\\ &=& \displaystyle{\lim_{h \rightarrow 0} \frac{1}{(2-x-h)(2-x)}}\\\\ &=& \displaystyle{\frac{1}{(2-x)^2}}\\\\ \end{array}$$As such, $\displaystyle{\lim_{x \rightarrow 1^-} f'(x) = \lim_{x \rightarrow 1^-} 1 = 1}$ and $\displaystyle{\lim_{x \rightarrow 1^+} f'(x) = \lim_{x \rightarrow 1^+} \frac{1}{(2-x)^2} = 1}$.
As these agree and $f(x)$ is continuous at $x=1$, $f(x)$ is also differentiable at $x=1$.
Finally, we look at the derivatives of the various "pieces", lest they are undefined at any additional relevant $x$-values. Note the following can be quickly verified with the limit definition of the derivative:
$$\frac{d}{dx}(-2x) = -2; \quad \frac{d}{dx}(-x) = -1; \quad \frac{d}{dx} (x) = 1; \quad \frac{d}{dx} \left( \frac{1}{2-x} \right) = \frac{1}{(2-x)^2}$$Seeing no domain issues in the derivatives above, except $x = 2$ which has already discussed, we conclude $f(x)$ is differentiable for all $x$ except $x=2,-1$, and $0$.
Given the following function, $$f(x) = \left\{ \begin{array}{ccc} -\sqrt{16-x^2} &,& x \lt 0\\\\ 3 &,& x = 0\\\\ x^2-4 &,& 0 \lt x \le 3\\\\ 3+\sqrt{7-x} &,& x \gt 3 \end{array} \right.$$
Sketch the graph of $y=f\,(x)$
For what values of $x$ does $f\,'(x)$ not exist? Explain.
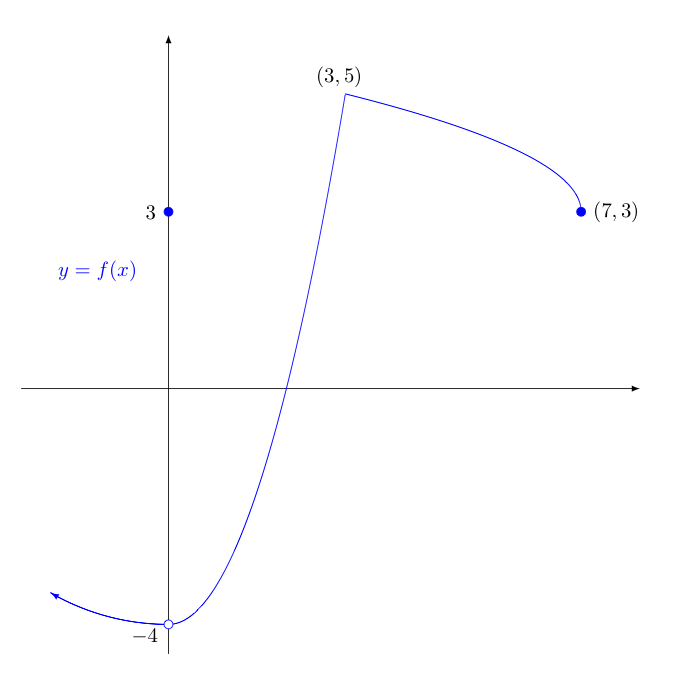
$f$ is not differentiable at $x=-4$ due to a removable hole discontinuity at $(0,-4)$
$f$ is not differentiable at $x=3$ as there is a corner (the left and right limits for $f'(x)$ as $x \rightarrow 3$ disagree)
$f$ is not differentiable at $x=7$ in part because the domain ends there, so one can't approach $x=7$ (from both sides) in the limit definition of the derivative -- but also because the left limiting value of the derivative at $x=7$ is $-\infty$ (so on the left, there is a vertical tangent).