

 |  |
Often, one has a relationship (i.e., an equation) between two or more variables that is valid at any point in time. If one implicitly differentiates (most frequently with respect to time) both sides of this equation governing the relationship between the variables, one produces another equation that relates the rates of change for the variables involved.
This resulting equation can frequently be solved for an unknown rate at some particular instant in time if the values of some of the other rates are known.
The solutions to the following problems (known as related rate problems) provide some examples of this process:
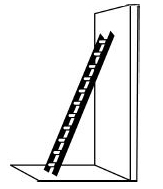 A 20 ft long ladder is leaning against a wall. If the bottom of the ladder is pulled away at a rate of 2 ft/s, how fast is the top of the ladder falling when it is 12 ft above the ground?
A 20 ft long ladder is leaning against a wall. If the bottom of the ladder is pulled away at a rate of 2 ft/s, how fast is the top of the ladder falling when it is 12 ft above the ground?
For any time $t$, let $y$ be the height of the ladder on the wall, and $x$ be the distance from the wall to the bottom of the ladder.
We are given the rate $\frac{dx}{dt} = 2$ ft/s.
We seek the unknown rate $\frac{dy}{dt}$.
Note that at any instance in time, $x$ and $y$ are related by the Pythagorean theorem,
$$x^2+y^2 = 20^2$$Differentiating the above implicitly, with respect to time $t$, we introduce the desired derivatives
$$2x \cdot \textstyle{\frac{dx}{dt}} + 2y \cdot \textstyle{\frac{dy}{dt}} = 0$$Now, noting that at the instant in which we are interested:
$$\begin{array}{l} y = 12\\ x^2+12^2 = 20^2\\ \textrm{and thus, } x = \sqrt{400-144} = 16 \end{array}$$Plugging this information and the known rate into the equation above that relates the rates, we have
$$2(16)(2) + 2(12)\cdot \textstyle{\frac{dy}{dt}} = 0$$which we can solve for $\frac{dy}{dt}$.
$$\textstyle{\frac{dy}{dt}} = \displaystyle{-\frac{8}{3}} \textrm{ ft/s}$$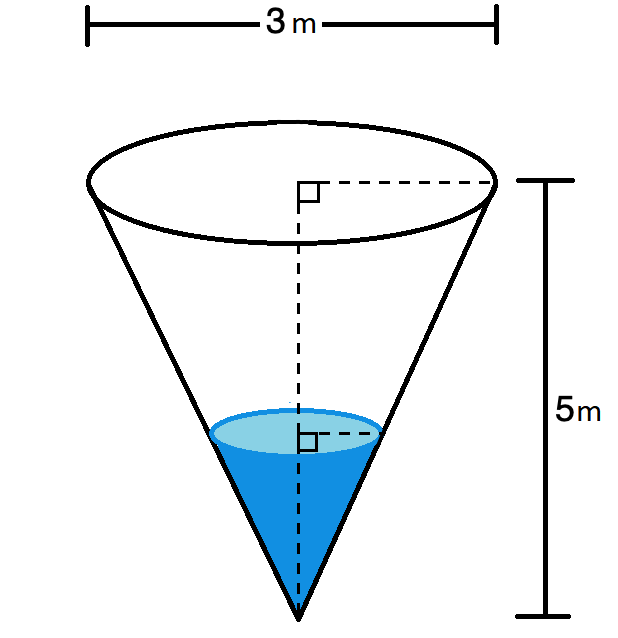 Fill a conical cup, 5 in high, 3 in across the top at a rate of 2 in3 per minute. How fast is the water rising when the cup is half full?
Fill a conical cup, 5 in high, 3 in across the top at a rate of 2 in3 per minute. How fast is the water rising when the cup is half full?
For any time $t$, let $h$ be the height of the water in the cup, $V$ be the volume of the water in the cup, and $r$ be the radius of the circle of water at height $h$.
We are given the rate $\frac{dV}{dt} = 2$ in3.
We seek the unknown rate, $\frac{dh}{dt}$.
Note that $V$ and $h$ are related by the equation governing the volume of a cone,
$$V = \frac{\pi r^2 h}{3}$$Differentiating now with respect to time $t$ will introduce three derivatives ($\frac{dV}{dt}$,$\frac{dr}{dt}$, and $\frac{dh}{dt}$), two of which are unknown. Prefering to only introduce one unknown rate ($\frac{dh}{dt}$, the rate we seek), we attempt to eliminate the $r$ from the equation. Noting that $r = \frac{3h}{10}$ by similar triangles, we can do just that -- via substitution -- to find
$$V = \frac{3\pi}{100} \cdot h^3$$Now, when we differentiate implicitly, with respect to time $t$, we get
$$\textstyle{\frac{dV}{dt}} = \displaystyle{\frac{3\pi}{100}} \cdot 3h^2 \cdot \textstyle{\frac{dh}{dt}}$$Now, note that at the instant in which we are interested:
$$h=\frac{5}{2}$$Plugging this information and the known rate into the equation above relates the rates, we have
$$2 = \frac{3\pi}{100} \cdot 3\left(\frac{5}{2}\right)^2 \cdot \textstyle{\frac{dh}{dt}}$$Solving this for the unknown rate $\frac{dh}{dt}$, we find
$$\textstyle{\frac{dh}{dt}} = \displaystyle{\frac{32}{9\pi}} \textrm{ inches per minute}$$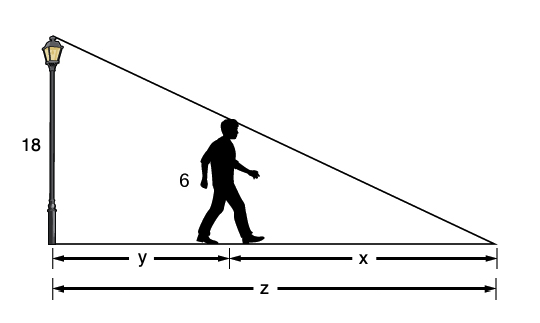 The light at the top of a 18 ft pole shines down on a 6 ft student who is walking away from the pole at a rate of 3 ft/s. Find the rate at which the length of the student’s shadow is
changing. How fast is the tip of the shadow moving?
The light at the top of a 18 ft pole shines down on a 6 ft student who is walking away from the pole at a rate of 3 ft/s. Find the rate at which the length of the student’s shadow is
changing. How fast is the tip of the shadow moving?
Let $x$ be the length of the shadow, $y$ be the distance between the student and the pole, and $z$ be the distance between the tip of the shadow and the pole.
We are given the rate $\frac{dy}{dt} = 3$ ft/s.
We first seek the unknown rate $\frac{dx}{dt}$ (the rate at which the shadow is growing)
Note that $x$ and $y$ are related by the equation below, derived from similar triangles.
$$\frac{x}{6} = \frac{x+y}{18}$$We can save ourselves some work by finding a more "differentiation-friendly" relation -- just cross-multiply, collect like terms, and divide by a common factor to find
$$2x = y$$Now, when we differentiate implicitly, with respect to time $t$, we get
$$2 \textstyle{\frac{dx}{dt}} = \textstyle{\frac{dy}{dt}}$$There is no instant of interest, but upon plugging in the known rate, we find
$$2 \cdot \frac{dx}{dt} = 3$$Solving this for the unknown rate $\frac{dx}{dt}$, we quickly find
$$\textstyle{\frac{dx}{dt}} = \displaystyle{3}{2} \textrm{ feet per second}$$Note, we can solve for how fast the tip of the shadow is moving in a similar manner.
The variables defined above and the known rate remain the same.
However, we now seek the unknown rate $\frac{dz}{dt}$ (the rate at which the shadow tip is moving).
Note that $x$, $y$, and $z$ are related by $z = x + y$
Differentiating this implicitly, with respect to time $t$, relates the rates in a way that introduces only a single unknown rate (i.e., $\frac{dz}{dt}$, the one we now seek):
$$\textstyle{\frac{dz}{dt} = \frac{dx}{dt} + \frac{dy}{dt}}$$There is again no instant of interest, but plugging in the known rates into the above, we have
$$\textstyle{\frac{dz}{dt}} = \displaystyle{\frac{3}{2} + 3 = \frac{9}{2} \textrm{ feet per second}}$$