

 |  |

Let us consider an example. Suppose a diagnostic test has probability $0.95$ of giving a positive result when applied to a person suffering from a certain disease, and a $0.10$ probability of giving a (false) positive) when applied to a person that does not suffer from the disease. Also suppose that it is estimated that $0.5\%$ of the population at any one time suffers from this disease. In a random screening, Alice tests positive for the disease. Clearly, before the screening and in absence of any additional information, the probability that Alice suffered from the disease was $0.005$. Once the screening has been performed and we now additionally know that Alice tested positive, how does the probability she suffers from the disease change? That is to say -- in light of this new information, what is the probability that Alice has the disease now?
Many people, when asked this question, will respond with "95%" -- but that is incorrect. Remember, the 95% previously mentioned is the probability that one tests positive given that the person suffers from the disease. We want the reverse. We want the probability that one suffers from the disease given that the test was positive.
To write things more succinctly -- if $A$ is the event of suffering from the disease, and $B$ is the event of testing positive, we know $P(B|A)$ and we want to calculate $P(A|B)$.
One may find it useful to visualize all the probabilities involved in tree form, as shown below.
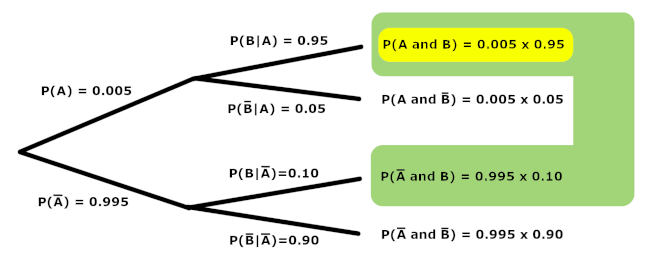
To find the probability $P(A|B)$, we focus on those cases where $B$ is known to be true (shown in green), and consider how likely it is that $A$ happens inside this reduced space (shown in yellow).
Of course, this results in the following formula, known as Bayes' Theorem:
$$P(A|B) = \frac{P(A)P(B|A)}{P(B)}$$For our particular example, we then have
$$P(\,\underbrace{\,\textrm{suffers from disease}\,}_A \, | \, \underbrace{\textrm{tests positive}}_B \,) = \frac{(0.005)(0.95)}{(0.005)(0.95) + (0.995)(0.10)} \doteq 0.0456$$One might note how counter-intuitively small the probability is of suffering from the disease given that one tests positive for it. This stems from the rarity of the disease in the population. Even 95% of the really small set of people that suffer from the disease is still small in comparison with 10% of a much larger set of people that don't.
Again, the applications for Bayes Theorem are far reaching -- including the areas of: genetics, linguistics, image processing, imaging, cosmology, machine learning, epidemiology, psychology, forensic science, evolution, and ecology. Alan Turing even used Bayesian logic to crack messages encrypted with the German enigma machines in the second World War!*

Suppose you're on a game show, and you're given the choice of three doors: Behind one door is a car; behind the others, goats. You pick a door, say No. 1, and the host, who knows what's behind the doors, opens another door, say No. 3, which has a goat. He then says to you, "Do you want to pick door No. 2?" Is it to your advantage to switch your choice?

Marilyn's response was that the contestant should switch to the other door, suggesting that contestants who switch have a $2/3$ chance of winning the car, while contestants who stick to their initial choice have only a $1/3$ chance. Many readers of vos Savant's column refused to believe switching increased one's chance of winning the car. Indeed, 10,000 of them -- including nearly 1,000 with PhDs -- wrote to the magazine, with most of them claiming Marilyn was wrong.
Of course, Marilyn vos Savant was correct -- and Bayes' Theorem can help us understand why...
The initial guess certainly had a $1/3$ chance of being right and a $2/3$ chance of being wrong, until Monty deliberately eliminates one wrong door. This introduces new information, so the probabilities must be updated.
Let us be specific with the events involved. Suppose that:
Let us follow the question posed to Marilyn and assume that we have initially picked the first door, after which Monty opens the third door to reveal a goat.
Let us also note that, since there are two goats, Monty can always find a door with a goat behind it that is not the one initially picked by the contestant. Consequently, he will never open a door he knows to have a car behind it (and of course, he will not open the door the contestant initially chooses).
Our intention is to use Bayes' Theorem to find out which is larger: $$P(A|E) = \frac{P(A) \cdot P(E|A)}{P(E)} \quad \textrm{ or } \quad P(B|E) = \frac{P(B) \cdot P(E|B)}{P(E)}$$ If the first is larger, we should stay with our initial choice of the first door. If the second is larger, we should switch.
Let us consider each of the values present in the two expressions above, in turn...
Of course, $P(A) = P(B) = 1/3$, as these probabilities do not take into account the new information (also called evidence) given to us by event $E$.
Also, $P(E)=1/2$ as Monty is either picking randomly between two doors with goats behind them both, or he is forced into picking one of two doors depending on the random placement of a car behind one of them.
$P(E|A) = 1/2$, as when $A$ is true (i.e., the car is behind the first door), Monty is picking randomly between showing the contestant what is behind door two or door three.
Finding $P(E|B)$ is where things get interesting. In this case, Monty can't pick door one, as that is what the contestant picked. Monty also can't pick door two, as we have been given knowledge that the car is behind this door (i.e., event B occurred). Thus, Monty must show us what is behind door three. Thus $P(E|B) = 1$.
Substituting all of these values into the two expressions resulting from Bayes' Theorem above, we have
$$P(A|E) = \frac{\frac{1}{3} \cdot \frac{1}{2}}{\frac{1}{2}} = \frac{1}{3} \quad \textrm{ and } \quad P(B|E) = \frac{\frac{1}{3} \cdot 1}{\frac{1}{2}} = \frac{2}{3}$$Thus, under these circumstances, the car is twice as likely to be behind door two as opposed to the first door.
Our initial selection of the first door and our assumption that Monty showed us a goat behind door three were arbitrary -- so without loss of generality, we will always be twice as likely to win the car if we switch from our initial guess!