

 |  |
Hypothesis testing is a decision-making process by which we analyze a sample in an attempt to distinguish between results that can easily occur and results that are unlikely.
One begins with a claim or statement -- the reason for the study. For example, the claim might be "This coin in my pocket is fair."
Then we design a study to test the claim. In the case of the coin, we might decide to flip the coin 100 times.
Consider what could happen as a result of flipping that coin 100 times:
Suppose we saw that 99 out of 100 times, the flip resulted in "heads". Upon seeing this, no one in their right mind would still believe that the coin was fair. That notion would be completely rejected. A fair coin should come up "heads" roughly 50% of the time. The probability that a fair coin would come up "heads" 99 times out of 100 is so ridiculously small, that for all practical purposes we should never see it happen. The fact that we saw it happen constitutes significant statistical "evidence" that an assumption the coin is fair is very, very wrong.
If on the other hand, if one saw 54 out of 100 flips result in "heads", then -- while this doesn't exactly match our expectation that a fair coin should come up heads 50 out of 100 times -- it is not that far off the mark. It may be that we have a fair coin and the amount we are off is just due to the random nature of coin flips. It may also be that our coin is only slightly unfair -- perhaps coming up heads only 55% of the time. We simply don't know. We have no evidence either way. There is no reason for a person who previously believed the coin was fair, to change their mind. There is no significant statistical "evidence" that the coin is not fair.
These two circumstances capture the essence of all hypothesis testing...
We hold some belief of something before we start our experiment or study (e.g., the coin is fair). This belief might be based on our experience or history. It might be the more conservative thing to believe, given two possibilities. It might be categorized as a "no-change-has-happened" belief. Whatever it is -- if we see a highly unusual difference between what is expected under the assumption of that belief and what actually happens as a result of our sampling or experimentation, we consequently reject that belief. Seeing a more common outcome under the assumption of that belief, however, does not result in any rejection of that belief.
Attaching some statistical verbiage to these ideas, the "belief" described in the previous paragraph is called the null hypothesis, $H_0$. The alternative hypothesis, $H_1$, is what one will be forced to conclude is more likely the case after a rejection of the null hypothesis.
These hypotheses are typically stated in terms of values of population parameters, with the null hypothesis stating that the parameter in question "equals" some specific value, while the alternative hypothesis says this parameter is instead either not equal to, greater than, or less than that same specific value, depending on the context.
Importantly, the "claim" (the reason for the study) might sometimes be the null hypothesis, while other times it might be the alternative hypothesis. A common error among students learning statistics for the first time is to assume the claim is always just one of these.
Returning to the example concerned with deciding whether a coin is fair or not based on flipping it 100 times, and assuming $p$ is the true proportion of heads that should be seen upon flipping the coin in our pocket, we first write the null and alternative hypotheses for our coin tossing experiment in the following way: $$H_0 : p = 0.50; \quad H_1 : p \neq 0.50$$
Recall that under the assumption of the null hypothesis, and as long as $np \ge 5$ and $nq \ge 5$, sample proportions $\widehat{p}$ should "pile up" in an approximately normal distribution with $$\mu = p = 0.5 \quad \textrm{ and } \quad \sigma = \sqrt{\frac{pq}{n}} = \sqrt{\frac{(0.5)(0.5)}{100}} = 0.05$$
Suppose as a result of our flipping the coin 100 times, we flipped heads $63$ times.
Then, the $z$-score for the corresponding sample proportion $\widehat{p} = 63/100 = 0.63$ is $$z_{0.63} = \frac{x - \mu}{\sigma} = \frac{0.63 - 0.5}{0.05} = 2.6$$ As a matter of verbiage -- for a hypothesis test involving a single proportion, the $z$-score associated with the sample proportion under consideration is called the test statistic. More generally, a test statistic indicates where on the related distribution the sample statistic falls.
Now we confront the question "Is what we saw unlikely enough that we should reject the null hypothesis? That is to say, does this particular observed $\widehat{p}$ happen so rarely when $p = 0.5$ that seeing it happen provides significant evidence that the $p \neq 0.5$?"
Towards this end, we consider the probability of seeing our test statistic, $z_{0.63} = 2.6$ -- or something even more extreme in the sense of the alternative hypothesis, in this standard normal distribution.
These "even more extreme" values (shaded red in the below diagram) certainly include those $z$ scores farther in the tail on the right (i.e., $z > 2.6$), but they also include those $z$-scores at a similar distance from the mean in the left tail of the distribution (i.e., $z < -2.6$). This is due to the fact that our alternative hypothesis simply says $p \neq 0.5$ -- it does not specify that $p$ is higher or lower than $0.5$. Had the alternative hypothesis been different, we might have limited ourselves to those $z$-scores in only one tail.
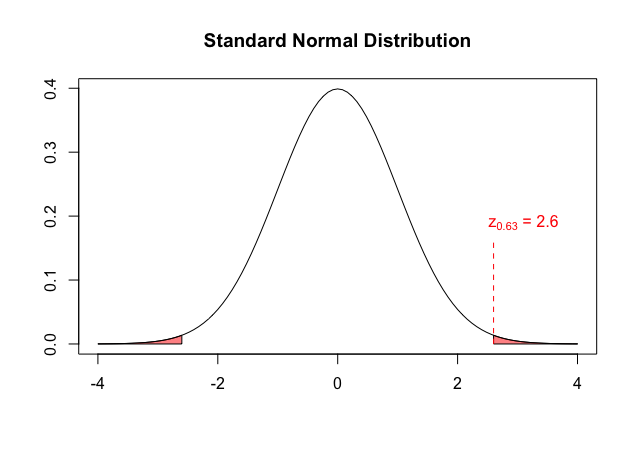
We can easily find $P_{\textrm{std norm}}(z < -2.6 \textrm{ or } z > 2.6)$ (i.e., the area shaded red above) with either a standard normal table, calculator, or a statistical programming environment like R.
As it turns out, $$P_{\textrm{std norm}}(z < -2.6 \textrm{ or } z > 2.6) \doteq 0.00932$$
Thus the probability, under the assumption that $p = 0.5$, that a sample will produce a $\widehat{p}$ as rare (or rarer) than what we saw in our one sample is only $0.00932$.
The probability just found is known as the p-value for the hypothesis test. More generally, the p-value is the probability of the observed outcome or an outcome at least that unusual (in the sense of the alternative hypothesis), under the assumption that the null hypothesis is true.
In this way, the p-value quantifies just how unusual what we saw actually was.
The question remains, however -- was the p-value we found small enough that we should conclude $p \neq 0.5$. (i.e., thus rejecting the null hypothesis)?
Understand that as long as the p-value is not zero, there is some possibility that $p = 0.50$ is actually true, and what we saw was just due to random chance. However, we want to make a decision -- one way or the other -- as to whether we believe this is a fair coin or not. We need to establish a cut-off probability, so that if the p-value is less than this cut-off, we consider the observed outcome unusual enough that it constitutes significant evidence that the null hypothesis should be rejected. This cut-off probability is called the significance level, and is denoted by $\alpha$.
As a standard, when a significance level is not specified at the outset, one typically uses $\alpha = 0.05$. Under this standard, observing something that happens less than 5% of the time is considered unusual enough to reject the null hypothesis.
Certainly, in this case we have $\textrm{p-value } \doteq 0.00932 < 0.05 = \alpha$ and the null hypothesis should be rejected. We indeed have statistically significant evidence that $p \neq 0.50$ and that the coin is consequently not a fair coin.
Continuing with our the previous example, note that if all we care about is making a decision as to whether or not we believe the coin is fair, then we don't actually need the exact value of the p-value -- we just need to know if it is less than the significance level, $\alpha$.
With this in mind, recall that we know in a standard normal distribution, by the Empirical Rule, roughly 95% of the distribution falls between $z = -2$ and $z = 2$. A slightly better approximation puts this 95% in the region where $-1.96 \lt z \lt 1.96$. That leaves 5% of the distribution in the tails, where $z < -1.96$ or $z > 1.96$ (i.e., the area outside the blue dashed lines below).
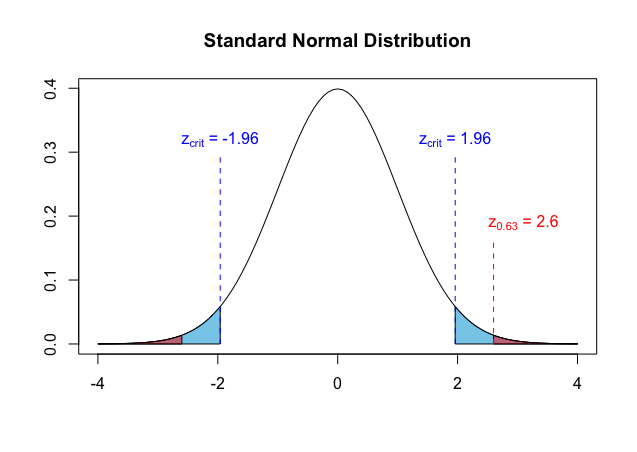
It should be patently obvious that if the test statistic (i.e., $z_{0.63} = 2.6$) falls in this region, the p-value (which agrees with the area of the red region above) must be smaller than 5%. Thus, we can immediately reject the null hypothesis, knowing $p \lt 0.05 = \alpha$.
The region of the distribution where it is unlikely for the test statistic to fall if the null hypothesis is indeed true (here, outside of $z = \pm1.96$) is called the rejection region, and the boundaries of the rejection region are known as critical values.
This (more traditional) way of performing a hypothesis test is certainly simpler to perform, especially in the absence of a calculator or software that can help with the calculation of the $p$-value. Although the lack of knowledge of the $p$-value makes comparing how significant results are relative to each other a bit more difficult.
There is one more way to perform a hypothesis test. It is only appropriate for two-tailed tests, but is simple to perform:
Simply find a confidence interval with confidence level of $(1-\alpha)$ where $\alpha$ is the significance level of the hypothesis test. Then, reject $H_0$ if the hypothesized population parameter (e.g., a proportion or mean) is not in the confidence interval.
This method of hypothesis testing can sometimes (very rarely) result in a different conclusion than the other two methods, as the confidence interval is built from an approximation of the standard deviation using the sample statistic ($\widehat{p}$, for example) as opposed to using the hypothesized population parameter (e.g. the proportion $p$ in the examples discussed here) to calculate the standard deviation.
Regardless of whether you use $p$-values, critical values, or confidence intervals to conclude whether or not the null hypothesis should be rejected -- once this is done, it is time to make an inference -- that is to say, it is time to communicate what your conclusion says about the original claim.
When forming an inference, one should try to phrase it in a manner easily digested by someone that doesn't know a lot about statistics. In particular, one should not use words like "null hypothesis", "p-value", "significance level", etc.
If the claim is the null hypothesis, you can start your inference with "There is enough evidence to reject the claim that..." if you rejected the null hypothesis, and with "There is not enough evidence to reject the claim that..." if you failed to reject the null hypothesis.
If the claim is the alternative hypothesis, you can instead start your inference with "There is enough evidence to support the claim that..." if you rejected the null hypothesis, and with "There is not enough evidence to support the claim that..." if you failed to reject the null hypothesis.
Alternatively, you can use phrases like "significantly different", "significantly higher", or "significantly lower" in the statement of your inference.
Very importantly -- one should never use the word "prove" in an inference. No matter the result of the hypothesis test, there is always a possibility of error. For example, at a significance level of $0.05$, one should absolutely expect that one in twenty experiments/observations will produce a p-value less than that $0.05$, which could then be erroneously deemed "statistically significant evidence" -- a point humorously driven home by this xkcd.com comic strip.
Indeed, there are two types of errors we could make when conducting a hypothesis test. We could -- as just described -- mistakenly reject a true null hypothesis (known as a Type I error), or we could also fail to reject a false hypothesis (known as a Type II error). Sadly, these firmly entrenched names for the types of errors one might commit are not very descriptive and consequently can easily be confused with each another. As a useful way to keep them straight, one might remember Aesop's fable of The Boy Who Cried Wolf". In part I of this story, the villagers commit a Type I error by reacting to the presence of a wolf when there is none. In part II of this story, the villagers commit a Type II error by failing to react when there actually is a wolf.
The probability of a Type I error is, of course, the significance level for the test, $\alpha$. The probability of a Type II error is denoted by $\beta$, and is impossible to calculate without actually knowing the actual value of the population parameter in question.
As one last bit of verbiage, the probability of rejecting a false null hypothesis is consequently $1 - \beta$, and is known as the power of the test. We can increase the power of a test by either increasing the sample size $n$, or the significance level, $\alpha$.