Tech Tips: Confidence Intervals for Proportions

Processing math: 100%

Tech Tips: Confidence Intervals for Proportions

Suppose $x$ elements of a sample of size $n$ have a certain characteristic. To find a confidence interval for the proportion of the population that has that characteristic, one first checks to see if the requisite assumptions are satisfied. Here, we determine if both $x$ and $n-x$ greater than or equal to 5. Then, presuming these assumptions are met, one can compute a confidence interval (with confidence level of $1-\alpha$ ) using $\widehat{p} \pm z_{\alpha/2} \sqrt{\frac{\widehat{p}\widehat{q}}{n}}$ We can, of course, leverage technology to make these same calculations,

R: The following custom function can be used to these ends:
```
ci.prop = function (x,n,conf) {
  # we check assumptions first..
  if ((x >= 5) & (n-x >= 5)) {
    p.hat = x/n
    q.hat = 1 - x/n
    z = qnorm(conf+(1.0-conf)/2.0)
    sd = sqrt(p.hat*q.hat/n)
    return (p.hat + c(-1,1)*z*sd)
  }
  else {
    print("assumptions not satisfied")
    return(NULL)
  }
}
```
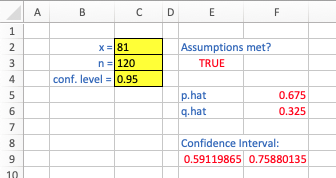
As an example, suppose one conducts a survey of $n = 120$ people and $81$ of them say that they will vote in the next election. Equivalently, of the $120$ surveyed, the proportion that said they would vote in the next election is $\widehat{p} = 0.675$ . If the above function has been defined in an R session, we can find a 95% confidence interval for the proportion that will vote in the next election with
```
ci.prop(x=81,n=120,conf=0.95)
[1] 0.5911986 0.7588014
```
Note if only 4 say they will vote in the next election, the function defined above realizes and reports that the assumptions behind the confidence interval construction are not satisfied:
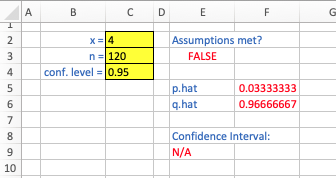
```
> ci.prop(x=4,n=120,conf=0.95)
[1] "assumptions not satisfied"
NULL
```
Excel: While there is not built-in function in Excel to do this, we can construct a worksheet to perform the desired calculations. Consider the example below, where the user enters the values of $x$ , $n$ , and the confidence level in cells $C2$ , $C3$ , and $C4$ , respectively:

Below are the relevant formulas for this sheet:
```
E3:"=AND(C2>=5,C3-C2>=5)"
F5:"=C2/C3"
F6:"=1-F5"
E9:"=IF(E3,F5+NORM.INV((1+C4)/2,0,1)*SQRT(F5*F6/C3),"N/A")"
F9:"=IF(E3,F5+NORM.INV((1+C4)/2,0,1)*SQRT(F5*F6/C3),"")"
```
Note the behavior of the sheet when the assumptions are not met: