Tech Tips: One-Sample Means Test

One-Sample Means Test ($\sigma$ unknown)

To conduct a $t$-test that a population's mean is $\mu$ given sample data and a confidence level, but with no knowledge of the population standard deviation $\sigma$,

R: use the function
```
t.test(data,alternative,mu,conf.level)
```
To explain the parameters:
- data is a vector consisting of the sample data
- mu is the mean $\mu$ associated with the null hypothesis
- alternative is a string of text that specifies the alternative hypothesis (i.e., "two.sided", "less", or "greater")
Consider the following example of this function's use:
Suppose the weights (in grams) of a sample of eleven small screws are found to be $$0.38,0.55,1.54,1.55,0.50,0.60,0.92,0.96,1.00,0.86,1.46$$ The production process for the screws is supposed to result in screws with mean weight of $1$ gram. Assuming the weights are normally distributed, test this claim at a $0.10$ significance level.
```
> data = c(0.38,0.55,1.54,1.55,0.50,0.60,0.92,0.96,1.00,0.86,1.46)
> t.test(data,alternative="two.sided",mu=1.00,conf.level=0.90)

    One Sample t-test

data:  data
t = -0.48485, df = 10, p-value = 0.6382
alternative hypothesis: true mean is not equal to 1
90 percent confidence interval:
 0.7070946 1.1692691
sample estimates:
mean of x
0.9381818
```
Given the $p$-value given above, which is greater than the significance level, this sample does not provide any statistically significant evidence that the mean weight is not $1$ g.

Additional Notes:

If all one wishes to calculate is the confidence interval for a population mean given a sample taken from it -- one can simply pass to t.test() the data and conf.level arguments and look at the conf.int component of the resulting list, as seen below.
```
> data = c(68,73,68,70,75,57,64,67,74,64,64,66,71,66,59,66)
> t.test(data,conf.level=0.95)$conf.int
[1] 64.35351 69.64649
attr(,"conf.level")
[1] 0.95
```
When conducting a one-tailed test, one should use alternative="less" or alternative="greater", as appropriate.

If one should desire to store the $p$-value in a variable to use for some other purpose, one can extract it from the overall test results in the following way:
```
> test.results = t.test(data,alternative="two.sided",mu=1.00,conf.level=0.90)
> test.results$p.value
[1] 0.6382267
```
Similarly, we can retrieve the upper and lower bounds of the related confidence interval with
```
> test.results = t.test(data,alternative="two.sided",mu=1.00,conf.level=0.90)
> test.results$conf.int[c(1,2)]
[1] 0.7070946 1.1692691
```

Excel: One can build a worksheet for conducting a one sample test concerning a mean when the population's standard deviation is unknown using the functions related to a $t$-distribution. Below is an example:

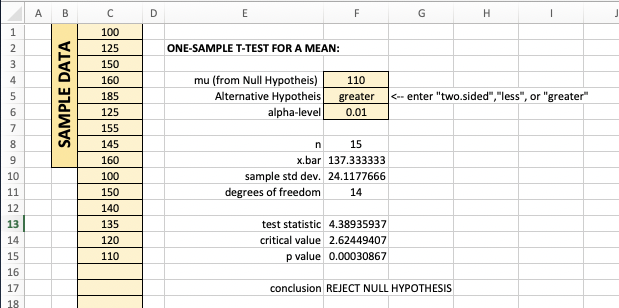
Here are the relevant formulas:

F8:"=COUNTA(C:C)"                              # the COUNTA() function counts non-empty 
F9:"=AVERAGE(C:C)"                             # cells in the range given to it
F10:"=STDEV.S(C:C)"
F11:"=F8-1"
F13:"=(F9-F4)/(F10/SQRT(COUNTA(C:C)))"

F14:"=IF(EXACT(TRIM(F5),"two.sided"),          # the TRIM() function removes extra spaces
         T.INV(F6/2,F11),
         IF(EXACT(TRIM(F5),"less"),            # the EXACT() function returns TRUE when 
            T.INV(F6,F11),                     # the two strings passed to it agree, and
            IF(EXACT(TRIM(F5),"greater"),      # FALSE otherwise
               T.INV(1-F6,F11),
               "ERROR")))"                     # the IF(condition,a,b) function returns
                                               # a when condition is TRUE, b otherwise
F15:"=IF(EXACT(TRIM(F5),"two.sided"),
        2*(1-T.DIST(ABS(F13),F11,TRUE)),
        IF(EXACT(TRIM(F5),"less"),
           T.DIST(F13,F11,TRUE),
           IF(EXACT(TRIM(F5),"greater"),
              1-T.DIST(F13,F11,TRUE),
              "ERROR")))"

F17:"=IF(F15<F6,"REJECT NULL HYPOTHESIS","FAIL TO REJECT NULL HYPOTHESIS")"