

 |  |
Modify the class Date given below so that it implements the Comparable interface in a reasonable way.
public class Date {
private final int month, day, year;
public Date(int m, int d, int y) {
month = m;
day = d;
year = y;
}
⋮
}
public class Date implements Comparable<Date> {
private final int month, day, year;
public Date(int m, int d, int y) {
month = m;
day = d;
year = y;
}
⋮
public int compareTo(Date that) {
if (this.year < that.year) return -1;
if (this.year > that.year) return 1;
if (this.month < that.month) return -1;
if (this.month > that.month) return 1;
if (this.day < that.day) return -1;
if (this.day > that.day) return 1;
return 0;
}
}
Show the state of an array with elements {f,b,a,h,c,d,g,e} ...
after each exchange in a selection sort.
after each sequence of exchanges required to accomplish each insertion in an insertion sort.
Order before selection sort application: f b a h c d g e 0 1 2 3 4 5 6 7 ------------------------ a b f h c d g e a b f h c d g e a b c h f d g e a b c d f h g e a b c d e h g f a b c d e f g h a b c d e f g h a b c d e f g h Order after selection sort application: a b c d e f g h
Order before insertion sort application: f b a h c d g e 0 1 2 3 4 5 6 7 ------------------------ f b a h c d g e b f a h c d g e a b f h c d g e a b f h c d g e a b c f h d g e a b c d f h g e a b c d f g h e a b c d e f g h Order after insertion sort application: a b c d e f g h
What is the average runtime cost (in terms of comparisons made) for an insertion sort of $n$ elements in Big-O notation?
$O(n^2)$
What is the best case and worst case time complexity (in terms of comparisons made) in Big-O notation for the selection sort algorithm? Then, answer this same question with regard to exchanges made.
comparisons: $O(n^2)$; exchanges: $O(n)$
Suppose myData references the following sorted array. One wishes to determine if 37 is in the array using a binary search. List the indices of the array elements compared with 37 in the course of doing this binary search.
$$\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|}\hline
0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 & 13 & 14\\\hline
11 & 15 & 19 & 21 & 22 & 25 & 27 & 30 & 34 & 35 & 36 & 39 & 40 & 42 & 50\\\hline
\end{array}$$
7, 11, 9, 10
Suppose myLetters references either a list or array containing the letters below in the order shown..
$$\begin{array}{|c|c|c|c|c|c|c|c|}\hline
G & A & F & B & D & H & E & C\\\hline
\end{array}$$
Trace the application of each sorting algorithm indicated below to the above array by showing the order of the letters after
each swap/exchange applied during a selection sort. To the side of each order you provide, include the candidates considered for the relevant minimum value for the pass in question.
each sequence of swaps/exchanges required to accomplish each "insertion" during an insertion sort. To the side of each order you provide, indicate how many swaps were made to accomplish the insertion in question. You do not need to show the individual swaps, however.
GAFBDHEC | GA AGFBDHEC | GFB ABFGDHEC | FDC ABCGDHEF | GD ABCDGHEF | GE ABCDEHGF | HGF ABCDEFGH | G ABCDEFGH |
GAFBDHEC AGFBDHEC | 1 AFGBDHEC | 1 ABFGDHEC | 2 ABDFGHEC | 2 ABDFGHEC | 0 ABDEFGHC | 3 ABCDEFGH | 5
When is an insertion sort better than a selection sort? When is a selection sort better than an insertion sort?
Insertion sort can better than selection sort when the list is partially sorted, while selection sort can be better than insertion sort when exchanges/swaps are expensive (e.g., in terms of time or memory space).
Show the state of the array after each merge in a merge sort of array containing the following elements in the order given below:
'M', 'I', 'D', 'S', 'P', 'A', 'C', 'E'
Order before mergesort application: M I D S P A C E 0 1 2 3 4 5 6 7 ------------------------ I M D S P A C E D I M S P A C E D I M S A P C E D I M S A C E P A C D E I M P S
Name three improvements that can be made to the basic merge sort algorithm.
Use insertion sort for small subarrays (typically less than 10 elements long, to reduce recursive overhead)
Check to see if merging is necessary (by comparing the two "middle" elements)
Eliminate the copy to the auxiliary array (by switching the role of the initial and auxiliary array with each recursive call)
Prove that the cost/complexity function $C(n)$ for merge sort in terms of array assignments has the property $C(n) \sim n\log_2 n$. You may begin your proof with the assumption that $C(1) = 0$ and $C(n) = 2C(n/2) + n$ for all other $n > 1$.
See the notes here.
When using the element at index $0$ as the pivot and Hoare's "ends-to-middle" partitioning, at what index is the pivot ultimately placed in an array of 15 equal values?
The pivot is ultimately placed at index $7$.
Given the following array, show the state of the array after each swap/exchange when the quicksort algorithm using Hoare's "ends-to-middle" partitioning is applied. For swaps/exchanges that result in placing a pivot in its final location, indicate the lowest and highest indices of the subarray currently being partitioned and the index where the pivot was placed. Conduct your sort without any initial shuffle or other "improvements".
$$\begin{array}{|c|c|c|c|c|c|c|c|}\hline P&I&V&O&T&A&N&G\\\hline \end{array}$$
lo pivot hi 0 1 2 3 4 5 6 7
-------------------------------------
P I V O T A N G
P I G O T A N V
P I G O N A T V
0 5 7 A I G O N P T V
0 0 4 A I G O N P T V
1 2 4 A G I O N P T V
3 4 4 A G I N O P T V
6 6 7 A G I N O P T V
Note, you can practice similar problems here
Why is it better to shuffle an array before sorting it with the quicksort algorithm?
This reduces the chances of the worst-case scenario for the time complexity of quicksort happening (i.e., when the elements are already in order and repeated pivots end up at the end of the subarrays for which they were chosen.) As such, shuffling first increases the chances that the resulting subarrays to the left and right of the pivot after partitioning will be approximately the same size -- which in turn means that the sorting can be done much more quickly.
Up to a constant multiplier, what is the best lower bound for the number of comparisons required by any comparison-based sorting algorithm to sort $n$ elements?
$n \ln n$
A new sorting algorithm, called "$X$-sort", is used to sort pairs of positive integers by the magnitudes of the products they form. Initially, the array of pairs has the following order:
(2,6), (1,2), (2,10), (2,2), (3,4), (5,4)
(1,2), (2,2), (3,4), (2,6), (5,4), (2,10)
Note that (2,6) and (3,4) are "equal" in terms of the magnitudes of the products they form, but appear in a different order after the sort has been applied. Hence, "$X$-sort" is not stable.
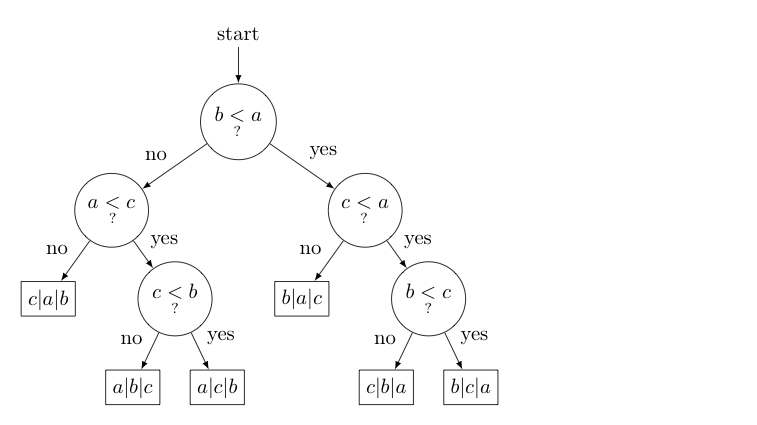
Suppose that the following 6 sequences of comparisons are made during a new comparison-based sorting technique when applied to various arrays of the form $\displaystyle{\begin{array}{|c|c|c|}\hline a & b & c\\\hline\end{array}}$. Note that the $a$, $b$, and $c$ in the array represent variable names, not characters -- so it could be the case that $a \gt c$ or $c \gt a$ depending on the values of those variables.
In each sequence, for each comparison made certain actions are taken that ultimately lead to the sorted order shown below each sequence. Draw the related decision tree.
b < a? no a < c? no c|a|b |
b < a? no a < c? yes c < b? no a|b|c |
b < a? no a < c? yes c < b? yes a|c|b |
b < a? yes c < a? no b|a|c |
b < a? yes c < a? yes b < c? no c|b|a |
b < a? yes c < a? yes b < c? yes b|c|a |
Which of the following is the least costly way to sort an already sorted array?
An insertion sort on an already sorted array uses only $\sim n$ comparisons, no exchanges, and accomplishes the sort in-place and in a stable way. Without pre-shuffling, an already sorted array is quicksort's worst case with $\sim n^2/2$ comparisons.
With pre-shuffling, quicksort will still need $\sim 2n \log_2 n$ comparisons, slightly fewer exchanges, and is not stable (although it is done in-place).
The merge sort similarly requires $\sim n \log_2 n$ comparisons, twice the memory space -- assuming an auxiliary array the size of the original is created, and require lots of copying of array elements (although it is a stable sort).
While for large arrays, quicksort and merge sort typically crush insertion sort in terms of performance, in this odd circumstance, insertion sort is the clear winner.
Create a class BubbleSorter that implements the Sorter interface, where the sorting done by the required sort() method is implemented with a bubble sort.
Implement a bubble sort on a singly-linked list that keeps only a reference to the head of the list.
Create a class MergeSortNR that implements the Sorter interface, where the sorting done by the required sort() method is implemented with a non-recursive merge sort.
The non-recursive and recursive versions of merge sort are very similar -- except that in a non-recursive mergesort, one starts with a pass of 1-by-1 merges (merge adjacent subarrays of size 1, to make subarrays of size 2), then one makes a pass of 2-by-2 merges (merge adjacent subarrays of size 2 to make subarrays of size 4), then 4-by-4 merges, and so forth, until we do a merge that encompasses the whole array.
The non-recursive merge sort should outperform the recursive merge sort due to less overhead due to recursive calls. Run the class SortTester to compare the MergeSortNR you just wrote to other sorting methods, as found in InsertionSorter, SelectionSorter, MergeSorter, and QuickSorter, to see how your implementation compares.
In the SorterTest class, all of the sorting methods are applied to random arrays of various sizes (all powers of 2) one hundred times each, and the total times required for sorting by each method are reported for each array size.
Note: in order to collect execution times, SortTester uses the Stopwatch class.
Tweak the code in your MergeSortNR class until it generally does better than the MergeSort class (at least for larger-sized arrays). Times seen will vary, depending on many factors -- including the type of machine on which your code is executed. However, a sample run is shown below.
$ java SortTester↵
Size Ins Sel Mrg MrgNR Quick
4 0.001 0.000 0.000 0.000 0.003
8 0.000 0.001 0.000 0.002 0.000
16 0.003 0.001 0.001 0.000 0.004
32 0.000 0.003 0.000 0.003 0.005
64 0.004 0.004 0.008 0.003 0.001
128 0.015 0.012 0.013 0.003 0.005
256 0.045 0.059 0.013 0.014 0.027
512 0.056 0.070 0.004 0.003 0.008
1024 0.103 0.094 0.009 0.015 0.013
2048 0.402 0.377 0.025 0.031 0.030
4096 1.650 1.480 0.073 0.065 0.048
8192 6.718 6.144 0.137 0.136 0.110
When you are done, plot the results in a graph. (You can use Google SpreadSheet, Microsoft Excel, OpenOffice Calc, or other tools to this end). Does what you see agree with the Big-O analysis of each of these algorithms' average running times?
Complete the class Quick3WaySorter which implements the Sorter interface and uses 3-Way Quicksort partitioning to sort the array, and shows the state of the array after each partition, as suggested in the sample run provided below.
$ java Quick3WaySorter↵ Enter a string of characters to sort: PABXWPPVPDPCYZ [A, B, C, D, P, P, P, P, P, V, W, Y, Z, X] [A, C, D, B, P, P, P, P, P, V, W, Y, Z, X] [A, B, C, D, P, P, P, P, P, V, W, Y, Z, X] [A, B, C, D, P, P, P, P, P, V, Y, Z, X, W] [A, B, C, D, P, P, P, P, P, V, W, X, Y, Z] [A, B, C, D, P, P, P, P, P, V, W, X, Y, Z]
In addition using lo and hi to indicate the positions of the left-most and right-most ends of the section of the array a[] that we are partitioning, keep track of 3 more positions:
Then, simply compare the pivot with the element of the array at this last position; make an appropriate exchange if warranted; and update these three values, as needed.
Complete the class QuickSorterWithFewerRecursiveCalls by adding bodies to its private implementations of sort1() and sort2() methods that both conduct a quicksort of the array in question, but do so using only a single recursive call in sort1() [To clarify, this means a call to sort1() that only sorts one side recursively (e.g., always the left side) -- it is ok to have this one call to sort1 in a loop, however.] and without any recursive calls in sort2(). Interestingly, this makes sort2() a fully iterative implementation of quicksort! Do not add any additional instance or static variables and/or methods. Confine your additions to the bodies of the two aforementioned private methods.
A sample run is shown.
$ java QuickSorterWithFewerRecursiveCalls↵
Sorted (w/ 1 recursive call): [A, C, E, E, I, K, L, M, O, P, Q, R, S, T, U, X]
Sorted (iterative quicksort): [A, C, E, E, I, K, L, M, O, P, Q, R, S, T, U, X]
For sort1(), notice that after recursively sorting the first half of the list, one repeatedly just does the same thing to what is left. For sort2(), note that you have been provided a stack -- might putting pairs of things on this stack help?
Complete the class SortableList by adding code in the locations indicated in this file. The class should use a (recursive) quicksort algorithm applied to a singly-linked list (not an array) with an appropriate partitioning scheme to accomplish calls to its sort() method.
With the supplied main() method, the output should agree with the sample run shown below:
$ java SortableList↵
g->h->n->r->u->y
a->b->d->e->i->m->o->r->s->t->u->x
b->e->i->m->o->s->z
a->e->t
a->b->i->n->r->s
h->i->t->w
b->h->o->t
a->d->h->n->s